HOW TO DETERMINE IF A SEQUENCE IS ARITHMETIC

Question 1 :

Check whether the following sequences are in A.P.

(i) a - 3, a - 5, a -7,...

Solution :

Since the common difference area same, the given sequence is arithmetic progression.

(ii)  1/2, 1/3, 1/4, 1/5........

Solution :

The common differences are not equal. Hence the given sequence is not A.P.

(iii) 9, 13, 17, 21, 25,...

Solution :

The given sequence is arithmetic progression.

(iv) -1/3, 0, 1/3, 2/3.........

Solution :

(v) 1, -1, 1, -1, 1, -1,............

Solution :

The given sequence is not arithmetic progression.

How to Find Arithmetic Progression with 1st Term and Common Difference

Question 2 :

First term a and common difference d are given below. Find the corresponding A.P.

(i) a = 5 , d = 6

Solution :

General form of A.P

a, a + d, a + 2d,...........

5, (5+6), (5, + 2(6)), ......................

5, 11, 17, ...................

(ii) a = 7 , d = -5

Solution :

a, a + d, a + 2d,...........

a = 7

a + d  =  7 + (-5)  =  2

a + 2d  =  7 + 2(-5)  =  7 - 10  =  -3

The required sequence is 7, 2, -3, .................

(iii) a = 3/4, d = 1/2

Solution :

a = 3/4

a + d  =  (3/4) + (1/2)  =  (3+2)/4  =  5/4

a + d  =  (3/4) + 2(1/2)  =  (3/4) + 1  =  7/4

Hence the required sequence is 3/4, 5/4, 7/4,...............

Question 3 :

In an auditorium, the first row of seats has 30 seats. Each row behind the first row has 4 more seats than the row in front of it. How many seats are in the 25th row?

Solution :

Number of seats in the rows,

30, 30 + 4, 34 + 8, ...........

30, 34, 38, ............

Number of seats in the first row = 30

Difference between the consecutive rows = 4

Number of seats in the 25th row :

a_n = a + (n - 1) d

a₂₅ = 30 + (25 - 1) 4

= 30 + 24(4)

= 30 + 96

= 126

So, there are 126 seats in the 25th row.

Question 4 :

The first term of an arithmetic sequence is 3. The common difference of the sequence is 10 less than twice the first term. Write the next three terms of the sequence.

Solution :

First term (a) = 3

Common difference (d) = 2(3) - 10

= 6 - 10

= -4

a, a + d, a + 2d, ...............

3, 3 + (-4), 3 + 2(-4),...........

3, -1, -5, ............

Question 5 :

The volume (in cubic feet) of the water in a tank each hour after turning on a faucet can be estimated by the sequence in the table.

a. Write a function that represents the arithmetic sequence.

b. The tank is in the shape of a rectangular box. The length is 6 feet, the width is 3 feet, and the height is 2 feet. Find the nth term that represents a full tank. Explain.

Solution :

a)  a_n = a + (n - 1) d

a = 12, d = 15 - 12 ==> 3

a_n = 12 + (n - 1) 3

= 12 + 3n - 3

= 9 + 3n

b) Volume of box = length x width x height

= 6 x 3 x 2

= 36 cubic ft

a_n = 9 + 3n

9 + 3n = 36

3n = 36 - 9

3n = 27

n = 27/3

n = 9

Question 6 :

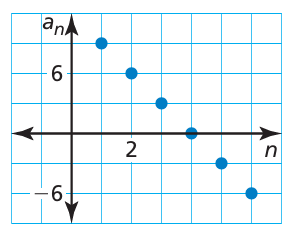
One term of an arithmetic sequence is a₁₉ = −45. The common difference is d = −3. Write a rule for the nth term. Then graph the first six terms of the sequence.

Solution :

a₁₉ = −45

a + 18d = −45

a + 18(-3) = -45

a - 54 = -45

a = -45 + 54

a = 9

a_n = a + (n - 1)d

a_n = 9 + (n - 1)(-3)

= 9 - 3n + 3

a_n = 12 - 3n

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.