HOW TO CHECK IF THE GIVEN POINTS ARE VERTICES OF RECTANGLE

(i) In a rectangle the length of opposite sides will be equal.

(ii) The rectangle can be divided into two right triangles.

(iii) If the given four vertices satisfies those conditions we can say the given vertices forms a rectangle.

Question 1 :

Examine whether the given points 

A(-3,2), B(4,2),  C (4,-3) and D (-3,-3)

forms a rectangle.

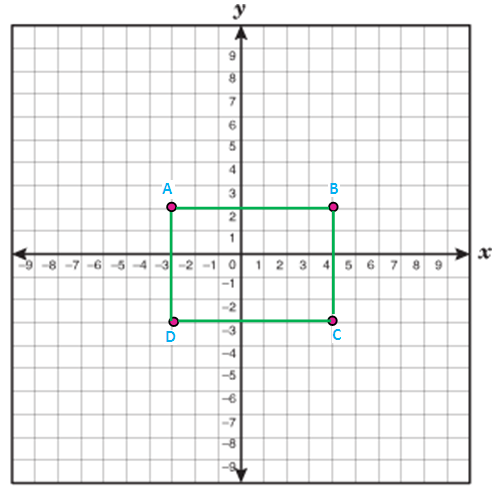
Solution :

Distance Between Two Points (x₁, y₁) and (x₂ , y₂)

√(x₂ - x₁)² + (y₂ - y₁)²

Length of AB :

Here x₁ = -3, y₁ = 2, x₂ = 4  and  y₂ = 2

=  √(4-(-3))² + (2-2)²

=  √(4+3)² 

=  √49

=  7 units

Length of BC :

Here x₁ = 4, y₁ = 2, x₂ = 4  and  y₂ = -3

=  √(4-4)² + (-3-2)²

=  √(-5)²

=  √25

=  5 units

Length of CD :

Here x₁ = 4, y₁ = -3, x₂ = -3 and  y₂ = -3

=  √(-3-4)² + (-3-(-3))²

=  √(-7)² + (-3+3)²

=  √49 + 0

=  7 units

Length of DA :

Here x₁ = -3, y₁ = 2, x₂ = -3 and  y₂ = 2

=  √(-3-(-3))² + (2-(-3))²

=  √(-3+3)² + (2+3)²

=  √0 + 5²

=  5 units

Length of AC :

Here x₁ = -3, y₁ = 2, x₂ = 4 and  y₂ = -3

=  √(4-(-3))² + (-3-2)²

=  √(4+3)² + (-5)²

=  √7² + 5²

=  √(49+25)

=  √74 units

In triangle ABC,

AC²  =  AB² + BC²

√74²  =  7² + 5²

74  =  49 + 25

74  =  74

So, the given points are vertices of rectangle.

Question 2 :

Examine whether the given points 

P(8, 3) Q(0, -1) R(-2, 3) and S(6, 7)

forms a rectangle.

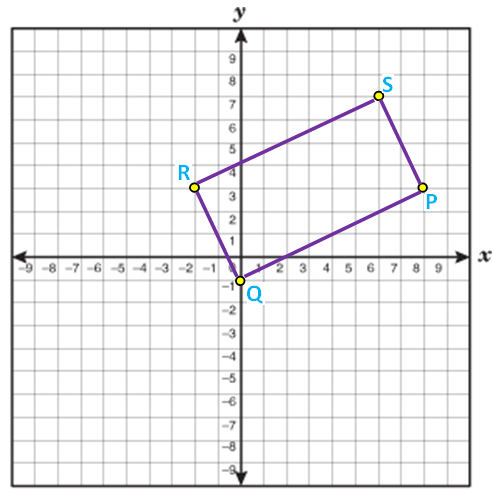
Solution :

Length of PQ :

Here x₁ = 8, y₁ = 3, x₂ = 0 and  y₂ = -1

=  √(0-8)² + (-1-3)²

=  √(-8)² + (-4)²

=  √(64+16)

=  √80

Length of QR :

Here x₁ = 0, y₁ = -1, x₂ = -2 and  y₂ = 3

=  √(-2-0)² + (3-(-1))²

=  √(-2)² + (3+1)²

=  √4 + 16

=  √20 units

Length of RS :

Here x₁ = -2, y₁ = 3, x₂ = 6 and  y₂ = 7

=  √(6-(-2))² + (7-3)²

=  √(6+2)² + 4²

=  √(64+16)

=  √80 units

Length of SP :

Here x₁ = 6, y₁ = 7, x₂ = 8 and  y₂ = 3

=  √(8-6)² + (3-7)²

=  √2² + (-4)²

=  √(4+16)

=  √20 units

Length of PR :

Here x₁ = 0, y₁ = -1, x₂ = 6 and  y₂ = 7

=  √(6-0)² + (7-(-1))²

=  √36 + 8²

=  √36 + 64

=  √100 units

In triangle QPS,

QS²  =  QP² + PS²

√100²  =  √80² + √20²

100  =  80 + 20

100  =  100

So the given vertices forms a rectangle.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.