HORIZONTAL AND VERTICAL SHIFTS WORKSHEET

Problems 1-3 : Refer the graph of f(x) given below.

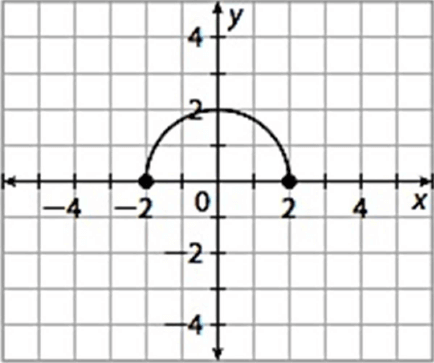
Problem 1 :

Sketch the graph of g(x) such that

g(x) = f(x) + 2

Problem 2 :

Sketch the graph of h(x) such that

h(x) = f(x + 2)

Problem 3 :

Sketch the graph of j(x) such that

j(x) = f(x - 2) - 3

Problems 4-6 : State the transformations on f(x) that woul create the graph of the new function described.

Problem 4 :

g(x) = f(x + 3) + 5

Problem 5 :

Problem 6 :

j(x) = -3 + f(x)

Problems 7-9 : The function f(x) has a domain of [-13, 4) and a range of [0, +∞). Find the domain and range for the functions.

Problem 7 :

g(x) = f(x + 4)

Problem 8 :

h(x) = f(x) + 25

Problem 9 :

h(x) = f(x - 3) - 7.5

Problems 10-12 : The point (8, -5) is on the graph of f(x). Find a point on the graph of the function.

Problem 10 :

g(x) = f(x - 13)

Problem 11 :

h(x) = f(x) - 17

Problem 12 :

h(x) = f(x + 3) + 5

Answers

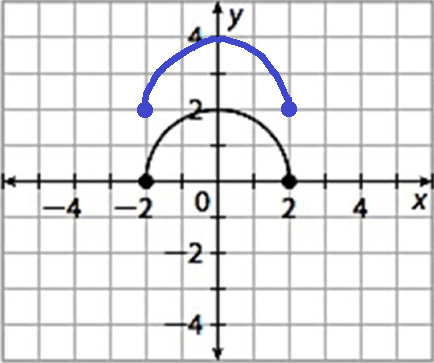
1. Answer :

g(x) = f(x) + 2

In f(x) + 2, 2 is added to f. So, there is a vertical shift of 2 units up.

To get the graph of g(x), the graph of f(x) has to be shifted 2 units up.

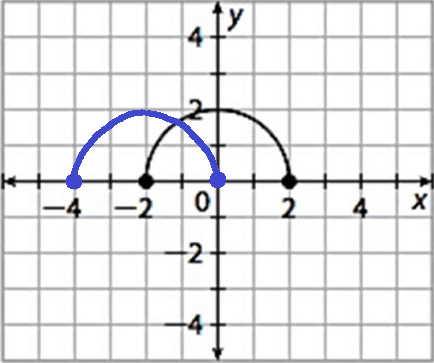
2. Answer :

h(x) = f(x + 2)

In f(x + 2), 2 is added to x. So, there is an horizontal shift of 2 units to the left.

To get the graph of h(x), the graph of f(x) has to be shifted 2 units to the left.

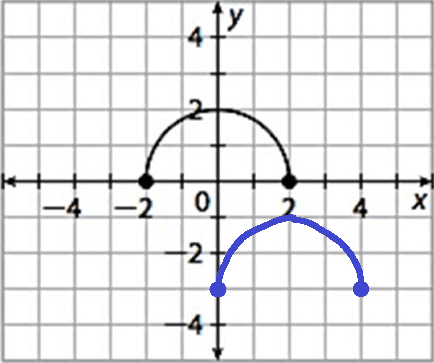
3. Answer :

j(x) = f(x - 2) - 3

In f(x - 2), 2 is subtracted from x. So, there is an horizontal shift of 2 units to the right.

In f(x - 2) - 3, 3 is subtracted from f. So, there is a vertical shift of 3 unit down.

To get the graph of j(x), the graph of f(x) has to be shifted 2 units to the right and 3 units down.

4. Answer :

g(x) = f(x + 3) + 5 

Horizontal Shift : 3 units to the left

Vertical Shift : 5 units up

5. Answer :

6. Answer :

j(x) = -3 + f(x)

j(x) = f(x) - 3

NO horizontal shift

Vertical Shift : 3 units down

7. Answer :

g(x) = f(x + 4)

Horizontal Shift :

4 units to the left

Since there is an horizontal shift of 4 units to the left, subtract 4 from the boundary values of the domain of f(x) to get the domain of g(x).

Domain of g(x) = [-13 - 4, 4 - 4)

= [-17, 0)

Vertical Shift :

NO vertical shift

Since there is NO vertical shift, there no change in range.

Range g(x) = [0, +∞)

8. Answer :

h(x) = f(x) + 25

Horizontal Shift :

NO horizontal shift

Since there is NO horizontal shift, there no change in range.

Domain of h(x) = [-13, 4)

Vertical Shift :

25 units up

Since there is a vertical shift of 25 units up, add 25 to the boundary values of the range of f(x) to get the range of h(x).

Range of h(x) = [0 + 25, +∞ + 25)

= [25, +∞)

Problem 9 :

h(x) = f(x - 3) - 7.5

9. Answer :

h(x) = f(x - 3) - 7.5

Horizontal Shift :

3 units to the right

Since there is an horizontal shift of 3 units to the right, add 3 to the boundary values of the domain.

Domain of j(x) = [-13 + 3, 4 + 3)

= [-10, 7)

Vertical Shift :

7.5 units down

Since there is a vertical shift of 7.5 units down, subtract 25 from the boundary values of the range.

Range of j(x) = [0 -7.5, +∞ - 7.5)

= [-.75, +∞)

Problems 10-12 : The point (8, -5) is on the graph of f(x). Find a point on the graph of the function.

Problem 10 :

g(x) = f(x - 13)

10. Answer :

g(x) = f(x - 13)

Horizontal Shift :

13 units to the right

Since there is an horizontal shift of 13 units to the right, add 13 to the x-coordinate of the point (8, -5).

Vertical Shift :

NO vertical shift

Since there is NO vertical shift, there no change in y-coodinate.

Therefore, the point on the graph of g(x) :

(21, -5)

Problem 11 :

h(x) = f(x) - 17

11. Answer :

h(x) = f(x) - 17

Horizontal Shift :

NO horizontal shift

Since there is NO horizontal shift, there no change in x-coordinate.

Vertical Shift :

17 units down

Since there is a vertical shift of 17 units down, subtract 25 from the y-coordinate of the point (8, -5).

Therefore, the point on the graph of h(x) :

(8, -22)

Problem 12 :

h(x) = f(x + 3) + 5

12. Answer :

h(x) = f(x + 3) + 5

Horizontal Shift :

3 units to the left

Since there is an horizontal shift of 3 units to the left, subtract 3 from the x-coordinate from the point (8, -5).

Vertical Shift :

5 units up

Since there is a vertical shift of 5 units up, add 5 to the y-coordinate of the point (8, -5).

Therefore, the point on the graph of j(x) :

(5, 0)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.