GRAPHING THE SOLUTIONS OF AN INEQUALITY

Example 1 :

Graph the solutions of the inequality y ≤ -3. Check the solutions.

Solution : 

Step 1 :

Draw a solid circle at -3 to show that -3 is a solution.

Step 2 :

Shade the number line to the left of -3 to show that numbers less than -3 are solutions.

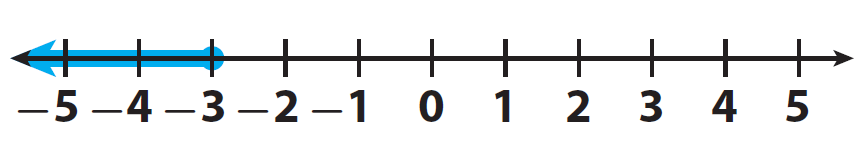
(Use a solid circle for an inequality that uses ≥ or ≤) 

Step 3 :

Check your solution. 

Choose a number that is on the shaded section of the number line, such as -4.

Substitute -4 for y.

-4 ≤ -3

-4 is less than -3, so -4 is a solution.

Step 4 :

Let us prove that -3 is a solution of the inequality y ≤ -3.

In the given inequality, plug y = -3. 

Then, we have 

-3 ≤ -3 ---> (-3 is less than or equal to -3)  ? 

Is the answer for the above question is "yes or "no" ? 

The answer for the above question is "Yes".

Because, -3 is equal to -3.

Hence, -3 is a solution to the inequality y ≤ -3. 

Example 2 :

Graph the solutions of the inequality 1 < m. Check the solutions.

Solution : 

Step 1 :

Draw an empty circle at 1 to show that 1 is not a solution.

Step 2 :

Shade the number line to the right of 1 to show that numbers greater than 1 are solutions.

(Use an open circle for an inequality that uses > or <) 

Step 3 :

Check your solution. 

Choose a number that is on the shaded section of the number line, such as 2.

Substitute -4 for y.

1 < 2

1 is less than 2, so 2 is a solution.

Step 4 :

Let us prove that 1 is not a solution of the inequality 1 < m.

In the given inequality, plug m = 1. 

Then, we have 

1 < 1 ---> (1 is less than 1)  ? 

Is the answer for the above question is "yes or "no" ? 

The answer for the above question is "No".

Because, 1 is equal to 1.

Hence, 1 is not a solution to the inequality 1 < m. 

Example 3 :

Graph the solutions of the inequality t ≤ -4. Check the solutions.

Solution : 

Step 1 :

Draw a solid circle at -4 to show that -4 is a solution.

Step 2 :

Shade the number line to the left of -4 to show that numbers less than -4 are solutions.

(Use a solid circle for an inequality that uses ≥ or ≤) 

Step 3 :

Check your solution. 

Choose a number that is on the shaded section of the number line, such as -5.

Substitute -5 for t.

-5 ≤ -4

-5 is less than -4, so -5 is a solution.

Step 4 :

Let us prove that -4 is a solution of the inequality t ≤ -4.

In the given inequality, plug t = -4. 

Then, we have 

-4 ≤ -4 ---> (-4 is less than or equal to -4)  ? 

Is the answer for the above question is "yes or "no" ? 

The answer for the above question is "Yes".

Because, -4 is equal to -4.

Hence, -4 is a solution to the inequality t ≤ -4.

Example 4 :

Graph the solutions of the inequality -3 ≤ n. Check the solutions.

Solution : 

-3 ≤ n or n ≥ -3

Step 1 :

Draw a solid circle at -3 to show that -3 is a solution.

Step 2 :

Shade the number line to the right of -3 to show that numbers greater than or equal to -3 is the solution.

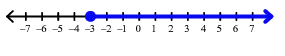
Step 3 :

Check your solution. 

Choose a number that is on the shaded section of the number line, such as -3.

n ≥ -3

Substitute -2 for n.

-2 ≥ -3

-2 is greater than -3. Then it is true.

Example 5 :

Solve the inequality and graph the solution

5 < (r + 9)/5

Solution : 

5 < (r + 9)/5

Multiplying by 5 on both sides, we get

25 < r + 9

Subtracting 9 on both sides

25 - 9 < r

16 < r

From the above inequality, we understand that the values of r should greater than 16. At 16, we have to draw the open or transparent circle.

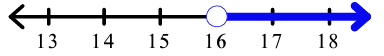
Example 6 :

Solve the inequality and graph the solution

63 < 4p - 3(-4p - 5)

Solution : 

63 < 4p - 3(-4p - 5)

Distributing -3, we get

63 < 4p + 12p + 15

63 < 16p + 15

Subtracting 15 on both sides

63 - 15 < 16p

48 < 16p

Dividing by 16 on both sides

48/16 < 16p/16

3 < p

All values of p should be greater than 3. So, at 3 we have to draw the transparent circle and shade the portion towards the right of 3.

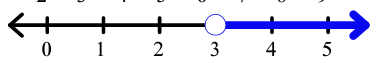
Example 7 :

Solve the inequality and graph the solution

-6(m + 5) + 8(3m + 3) ≤ -24

Solution : 

-6(m + 5) + 8(3m + 3) ≤ -24

Distributing -6 and 8, we get

-6m - 30 + 24m + 24 ≤ -24

-6m + 24m - 30 + 24 ≤ -24

18m - 6 ≤ -24

Adding 6 on both sides

18m ≤ -24 + 6

18m ≤ -18

Dividing by 18, we get

m ≤ -1

The values of m should be lesser than or equal to -1. So, we have to shade the values towards the left of -1 and at -1, we have to draw the solid circle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.