GRAPHING RATIONAL FUNCTIONS WITH HOLES

A rational function is a function which is a fraction where both numerator and denominator are polynomials.

That is, a ratio of two polynomials P(x) and Q(x), where the denominator Q(x) is not equal to zero.

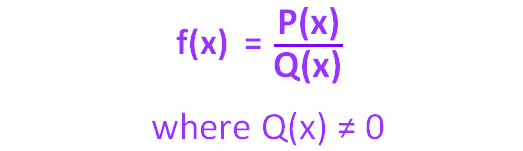
Before we learn, how to graph rational functions, first we have to be aware of the following stuff. 

1. Vertical Asymptote

2. Horizontal Asymptote

3. Slant Asymptote

4. Hole

Please click on each topic above to know more about the stuff.

Now let us look at an example to understand how to graph a rational function with hole through the following example. 

Example :

Graph the rational function given below.

f(x)  =  (x² - x - 2) / (x - 2)

Solution :

Step 1 :

First, we have to find hole, if any.

To find hole of the rational function, we have to see whether there is any common factor found at both numerator and denominator.

So, let us factor both numerator and denominator.

y  =  [(x - 2)(x + 1)] / (x - 2)

In our problem, clearly there is a common factor

(x - 2)

found in both numerator and  denominator.

So, there is a hole. 

Step 2 :

Now, we have to cross out the common factor (x - 2) at both numerator and denominator as given below.

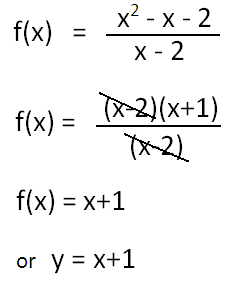
Step 3 :

Now we have to make the common factor (x - 2)  equal to zero.

When we do so, we get 

x - 2  =  0

x  =  2

So, the hole is at  x  =  2.

Step 4 :

After having crossed out the common factor (x - 2), the function is simplified to

f(x)  =  x + 1

or  

y  =  x + 1

Step 5 :

Substitute 2 for x  in y = x + 1.

y  =  2 + 1

y  =  3

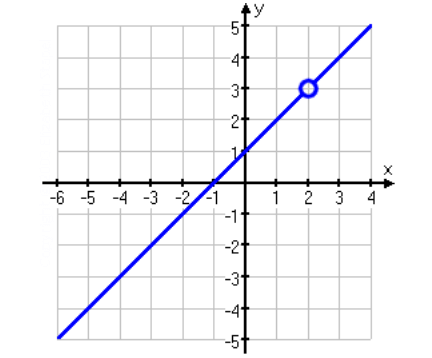
So, the hole appears on the graph at (2, 3).

Step 6 :

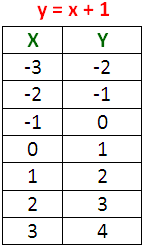
In y = x + 1, now we have to plug some random values for 'x' and find the corresponding values of 'y' as given in the table below.

Graph of the Given Rational Function

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.