HOW TO FIND THE HOLE OF A RATIONAL FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In this section, you will learn how to find the hole of a rational function
And we will be able to find the hole of a function, only if it is a rational function.
That is, the function has to be in the form of
f(x) = P/Q
Example : Rational Function
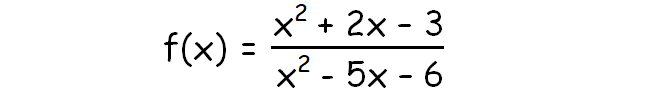
Steps Involved in Finding Hole of a Rational Function
Let y = f(x) be the given rational function.
Step 1 :
If it is possible, factor the polynomials which are found at the numerator and denominator.
Step 2 :
After having factored the polynomials at the numerator and denominator, we have to see, whether there is any common factor at both numerator and denominator.
Case 1 :
If there is no common factor at both numerator and denominator, there is no hole for the rational function.
Case 2 :
If there is a common factor at both numerator and denominator, there is a hole for the rational function.
Step 3 :
Let (x - a) be the common factor found at both numerator and denominator.
Now we have to make (x - a) equal to zero.
When we do so, we get
x - a = 0
x = a
So, there is a hole at x = a.
Step 4 :
Let y = b for x = a.
So, the hole will appear on the graph at the point (a, b).
Example 1 :
Find the hole (if any) of the function given below
f(x) = 1/(x + 6)
Solution :
Step 1:
In the given rational function, clearly there is no common factor found at both numerator and denominator.
Step 2 :
So, there is no hole for the given rational function.
Example 2 :
Find the hole (if any) of the function given below.
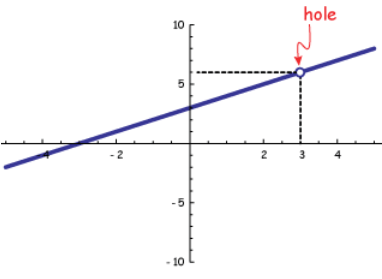
f(x) = (x2 + 2x - 3)/(x2 - 5x + 6)
Solution :
Step 1:
In the given rational function, let us factor the numerator and denominator.
f(x) = [(x + 3)(x - 1)]/[(x - 2)(x - 3)]
Step 2 :
After having factored, there is no common factor found at both numerator and denominator.
Step 3 :
Hence, there is no hole for the given rational function.
Example 3 :
Find the hole (if any) of the function given below.
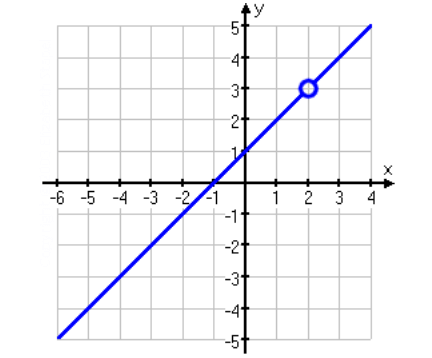
f(x) = (x2 - x - 2)/(x - 2)
Solution :
Step 1:
In the given rational function, let us factor the numerator.
f(x) = [(x - 2)(x + 1)]/(x - 2)
Step 2 :
After having factored, the common factor found at both numerator and denominator is (x - 2).
Step 3 :
Now, we have to make this common factor (x-2) equal to zero.
x - 2 = 0
x = 2
So, there is a hole at
x = 2
Step 4 :
After crossing out the common factors at both numerator and denominator in the given rational function, we get
f(x) = x + 1 ------(1)
If we substitute 2 for x, we get get
f(2) = 3
So, the hole will appear on the graph at the point (2, 3).
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

