HOW TO FIND HORIZONTAL ASYMPTOTE OF A FUNCTION

Horizontal Asymptote :

This is an horizontal line that is not part of a graph of a function but guides it for x-values 'far' to the right and/or 'far' to the left.

The graph may cross it but eventually, for large enough or small enough values of x, that is

x ---> ±∞

Always, the graph would get closer and closer to the horizontal asymptote without touching it.

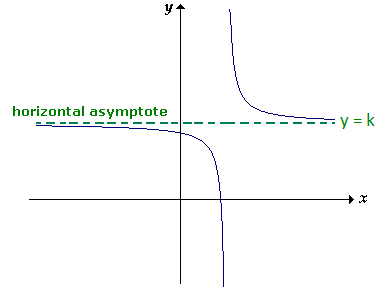
In the diagram above, y = k is an horizontal asymptote. Because, the graph is getting closer and closer to y = k without touching it as x ---> ±∞.

We can find horizontal asymptotes of a function, only if it is a rational function.

That is, the function has to be in the form of

f(x) = g(x)/h(x)

Rational Function - Example :

In each case, find the equation of horizontal asymptote.

Example 1 :

f(x) = 1/(x + 6)

Solution :

Step 1 :

In the given rational function, the largest exponent of the numerator is 0 and the largest exponent of the denominator is 1.

Step 2 :

Clearly largest exponent of the numerator is less than the largest exponent of the denominator.

So, equation of the horizontal asymptote is

y = 0 (or) x-axis

Example 2 :

f(x) = (x² + 2x - 3)/(x² - 5x + 6)

Solution :

Step 1 :

In the given rational function, the largest exponent of the numerator is 2 and the largest exponent of the denominator is 2.

Step 2 :

Clearly, the exponent of the numerator and the denominator are equal.

Step 3 :

Now, to get the equation of the horizontal asymptote, we have to divide the coefficients of largest exponent terms of the numerator and denominator.

So, equation of the horizontal asymptote is

y = 1/1

y = 1

Example 3 :

f(x) = (x² - 4)/(2x - 3)

Solution :

Step 1 :

In the given rational function, the largest exponent of the numerator is 2 and the largest exponent of the denominator is 1.

Step 2 :

Clearly, the largest exponent of the numerator is greater than the largest exponent of the denominator.

Step 3 :

Because the largest exponent of the numerator is greater than the largest exponent of the denominator, there is no horizontal asymptote.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.