GRAPHING A RATIONAL FUNCTION

A rational function is a function which is a fraction where both numerator and denominator are polynomials.

That is, a ratio of two polynomials P(x) and Q(x), where the denominator Q(x) is not equal to zero.

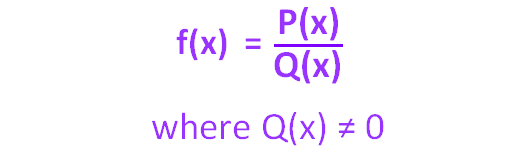
Before we learn, how to graph rational functions, first we have to be aware of the following stuff. 

1. Vertical Asymptote

2. Horizontal Asymptote

3. Slant Asymptote

4. Hole

Please click on each topic above to know more about the stuff.

Now let us look at an example to understand how to graph rational functions. 

Example :

Graph the rational function given below.

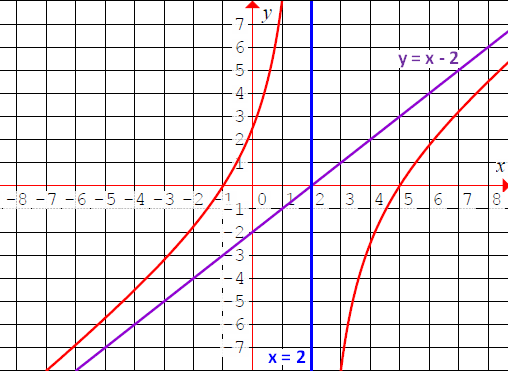
f(x)  =  (x² - 4x - 5) / (x - 2)

Solution :

Step 1 :

First, we have to find hole, if any.

To find hole of the rational function, we have to see whether there is any common factor found at both numerator and denominator.

So, let us factor both numerator and denominator.

y  =  [(x - 5)(x + 1)] / (x - 2)

In our problem, clearly there is no common factor found at both numerator and  denominator. So, there is no hole.

Step 2 :

Now, we have to find vertical asymptote, if any. 

Most of the rational function will have vertical asymptote. 

To find vertical asymptote, we have to make the denominator equal to zero.

Then, 

x - 2  =  0

x  =  2

So, the vertical asymptotes is

x  =  2

Step 3 :

Now we have to find horizontal asymptote, if any.

In the rational function given above, the highest exponent of the numerator is 2 and denominator is 1.

Clearly, the highest exponent of the numerator is greater than the highest exponent of the denominator

In a rational function, if the highest exponent of the numerator is greater than the highest exponent of the denominator, there is no horizontal asymptote.

So, there is no horizontal asymptote for the given rational function.

Step 4 :

Now we have to find slant asymptote, if any.

Clearly, the exponent of the numerator is greater than the exponent of the denominator by one. So, there is a slant asymptote.

To get the equation of the slant asymptote, we have to divide the numerator by the denominator using long division as given below.

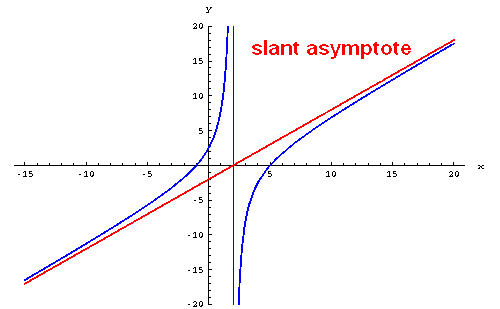
In the above long division, the quotient is (x - 2).

So, the equation of the slant asymptote is

y  =  x - 2

Step 5 :

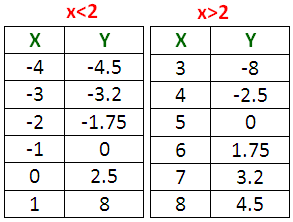
In the given rational function, now we have to plug some random values for 'x' and find the corresponding values of 'y'. 

We have already known that the vertical asymptote is

x  =  2 

Now, we have to take some random values for x in the following intervals. 

(x < 2),  (x > 2)

but not x = 2. 

(Because, x = 2 is vertical asymptote)

Step 6 :

In the slant asymptote y = x - 2, we have to plug some random values for 'x' and find the corresponding values of 'y'. 

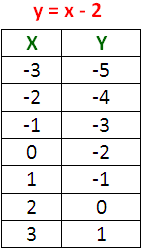
Graph of the Given Rational Function

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.