GEOMETRY PROBLEMS INVOLVING POLYNOMIALS

Set up an equation and hence find the value of x :

Problem 1 :

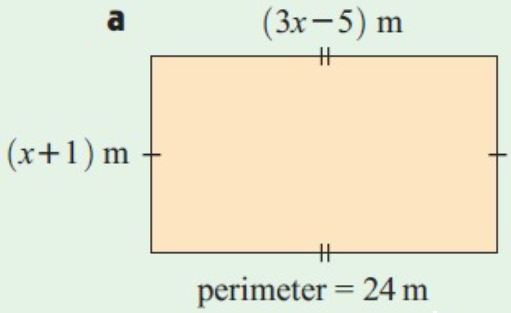
Solution :

Perimeter of rectangle  =  2 (l + w)

Let l and w be the length and width of the rectangle

Here, l =  3x - 5 and

w = x + 1

Perimeter of rectangle  = 24 m

2 (l + w)  =  24 

2(3x - 5 + x + 1)  =  24

6x – 10 + 2x + 2  =  24

8x – 8  =  24

8x  =  24 + 8

8x = 32

x  =  32/8

 x = 4

The value of x is 4.

Problem 2 :

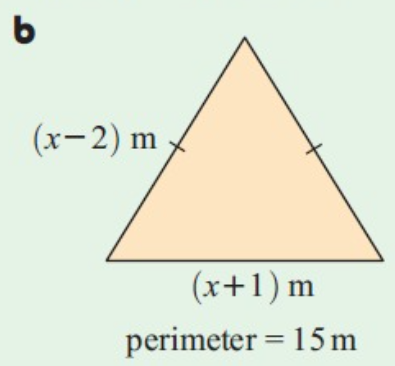
Solution :

Perimeter of triangle  =  a + b + c

Let a, b and c be the sides of the triangle respectively.

Perimeter =  15 m

Sum of all sides  =  15

x – 2 + x – 2 + x + 1  =  15

2 (x – 2) + (x + 1)  =  15

2x – 4 + x + 1  =  15

3x – 3  =  15

    3x =  15 + 3

3x  =  18

x  =   18/3

x  =  6 

The value of x is 6.

Problem 3 :

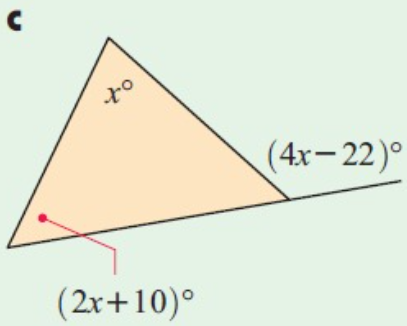
Solution :

Using exterior angles theorem,

x + (2x + 10)  =  (4x – 22)

x + 2x + 10  =  4x - 22

3x + 10  =  4x - 22

10 + 22  =  4x - 3

32  =  x

The value of x is 32.

Find the perimeter of the rectangle. Your answer must not contain x.

Problem 4 :

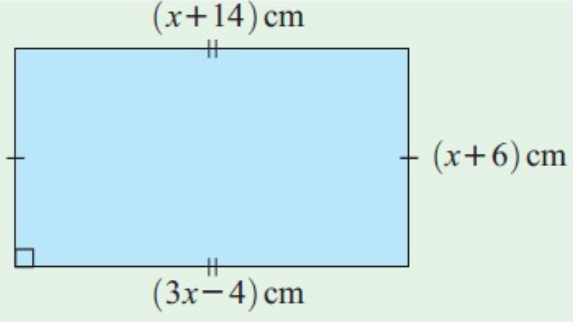
Solution :

Perimeter of rectangle  =  2 (l + w)

Let l and w be the length and width of the rectangle

Here, l  =  (3x - 4) cm and (x + 14) cm  and

w  =  (x + 6) cm

(3x - 4)  =  (x + 14)

3x – x  =  14 + 4

2x  =  18

x  =  9

(3x – 4) is the length of the rectangle.

l  =  3x – 4

l  =  3(9) – 4

l  =  27 – 4

l  =  23

  (x + 6) is the width of the rectangle.

w  =  x + 6

w  =  9 + 6

w  = 15

Perimeter of rectangle  =  2 (l + w)

=  2 (23 + 15)

=  2(38)

=  76

The Perimeter of rectangle  =  76 cm

Set an equation and hence find the value of x. 

Problem 5 :

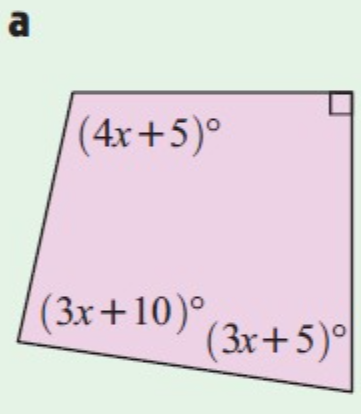
Solution :

The Sum of interior angles of a quadrilateral is 360º.

90 + 4x + 5 + 3x + 10 + 3x + 5  =  360

110 + 10x  =  360

10x  =  360 – 110

10x  =  250

x  =  250/10

x  =  25

The value of x  =  25

Problem 6 :

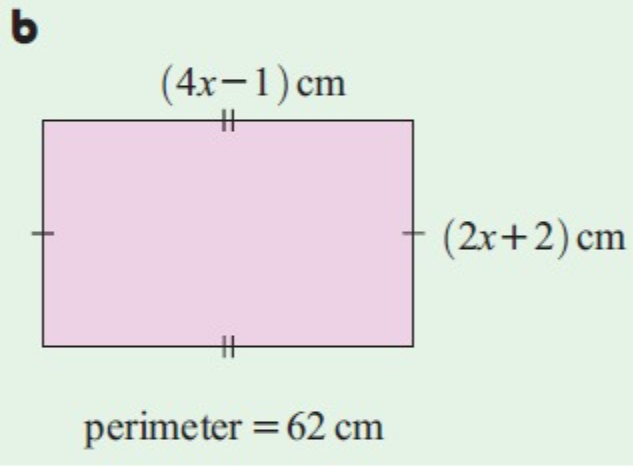
Solution :

Perimeter of rectangle  =  2 (l + w)

Let l and w be the length and width of the rectangle

Here , l  =  2x + 2 cm and

w  =  4x - 1 cm

perimeter of rectangle  =  62 cm

2 (l + w)  =  62

2 (2x + 2 + 4x -1)  =  62

2(6x + 1)  =  62

12x + 2  =  62

12x  =  62 – 2

12x  =  60

x  =  60/12

x  =  5 

The value of x is 5.

Problem 7 :

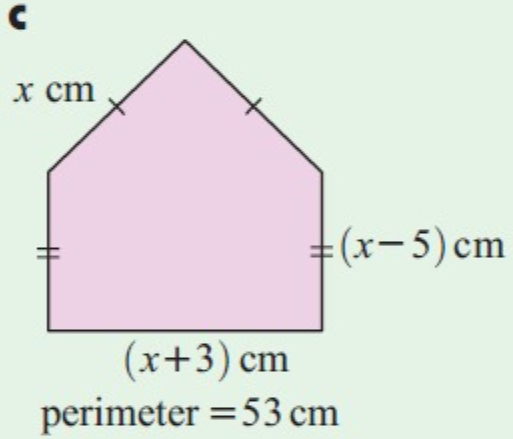
Solution :

x + x + x – 5 + x – 5 + x + 3  = 53

5x – 7  =  53

5x  =  53 + 7

5x  =  60

x  =  60/5

x  = 12

The value of x is 12.

Problem 8 :

Find x if the square and triangle have the same area :

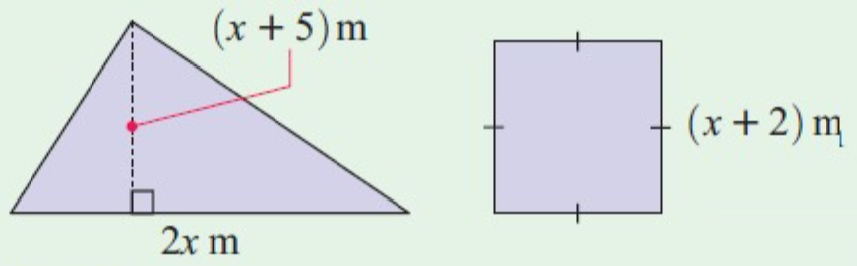
Solution :

area of square  =  area of triangle

a²  =  1/2 h b

(x + 2)²  =  1/2  (x + 5) · 2x

x² + 4 + 4 x  =  (x + 5) · x

x² + 4 + 4 x  =  x² + 5x

x² + 4 + 4x – x² – 5x

4 – x

x  =  4

Problem 9 :

Find x if both rectangles are having the same area :

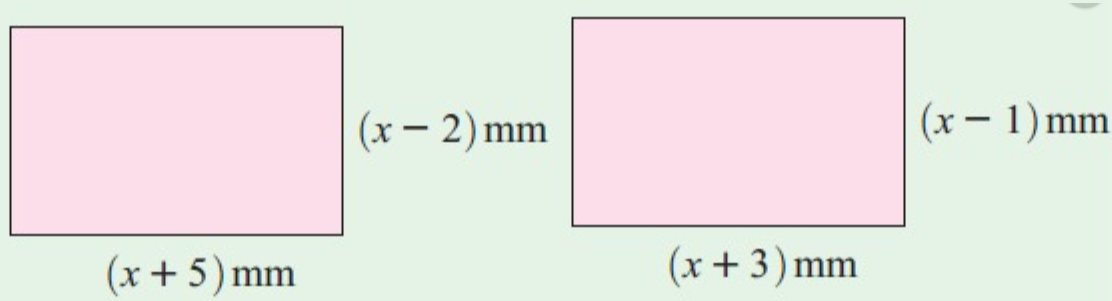
Solution :

Area of rectangles  =  l x w

  (x + 5) x (x – 2)  =  (x + 3) x (x – 1)

x² – 2x + 5x – 10  =  x² – x + 3x - 3

x² + 3x – 10  =  x² + 2x – 3

x² + 3x – 10  -  x² - 2x + 3  =  0

x – 7  =  0

x  =  7

Two rectangles have the same area.

Problem 10 :

A square courtyard has a side length of 50 yards. The city plans to add x yards to each side so that it can pour a sidewalk all the way around it. Write the expression that would represents the outside perimeter of the courtyard plus the sidewalk.

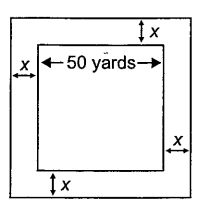
Solution :

The shape that we find inside is the square.

Side length of new square = 50 + x + x

= 50 + 2x

Perimeter of square = 4(side length)

= 4(50 + 2x)

= 200 + 8x

Problem 11 :

What is the expression that represents the area of the trapezoid shown ?

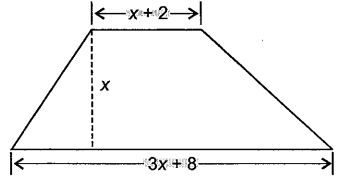
Solution :

Area of trapezium = (1/2) x h (a + b)

h = x, a = 3x + 8 and b = x + 2

a + b = 3x + 8 + x + 2

= 4x + 10

Area of trapezium = (1/2) ⋅ x ⋅ (4x + 8)

= (1/2) (4x² + 8x)

Problem 12 :

A square has an unknown side length x. A rectangle has a side length that is four feet longer than the square and a width that is two feet shorter than a square. The areas of both square and a rectangle are equal. Find the side length of the square.

Solution :

Side length of square = x

Side length of rectangle = x + 4

Width of the rectangle = x - 2

Area of square = area of rectangle

x² = (x + 4)(x - 2)

x² = x² - 2x + 4x - 8

2x - 8 = 0

2x = 8

x = 8/2

x = 4

So, the side length of the square is 4 inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.