FINDING UNKNOWN VERTICES WHEN AREA OF TRIANGLE IS GIVEN

Vertices of the triangle taken in order and their areas are given below. In each of the following find the value of a.

Problem 1 :

Whose vertices are (0, 0), (4, a) and (6, 4) and its area is 17 sq.units

Solution :

Area of the triangle  =  17 square units

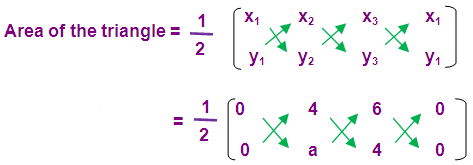
(1/2)[(0 + 16 + 0) – (0 + 6a + 0)] = 17

(1/2)(16 – 6 a) = 17

8 - 3a = 17

-3a = 9

a = -3

So, the value of a is -3.

Problem 2 :

The vertices are (a, a) , (4 , 5) and ( 6 , -1) and its area is 9 sq. units

Solution :

Area of the triangle  =  9 square units

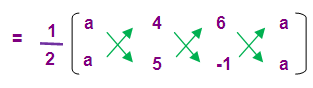
(1/2)[(5a - 4 + 6a) – (4a + 30 - a)]

(1/2)[(11a – 4) – ( 3a+30)]  =  9

(1/2)[11a – 4 – 3a - 30]  =  9

(1/2)[8a – 34]  =  9

4a – 17  =  9

4a  =  26

a  =  26/4

a  =  13/2

So, the value of a is 13/2.

Problem 3 :

The vertices are (a, -3),(3, a) and (-1, 5) and its area is 12 sq.units

Solution :

Area of the triangle = 12 square units

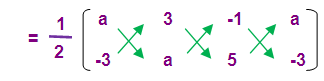
(1/2)[(a² + 15 + 3) – (-9 - a + 5a)]  =  12

(1/2)[(a² + 18 ) – (-9 + 4a)]  =  12

[a² + 18 + 9 - 4a]  =  12 x 2

a² - 4a + 27  =  24

a² - 4a + 27 -  24  =  0

a² - 4a + 3  =  0

(a - 1)(a - 3)  =  0

a  = 1, 3

So, the values of a are 1 and 3.

Vertices of given triangles are taken in order and their areas are provided aside. In each case, find the value of ‘p’.

Problem 4 :

The vertices are (0, 0), (p, 8), (6, 2) and has the area of 20 square units.

Solution :

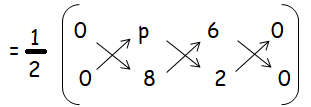
Area of triangle = (1/2) [(0 + 2p + 0) - (0 + 48 + 0)]

(1/2) [(0 + 2p + 0) - (0 + 48 + 0)] = 20 square units

(1/2)(2p - 48) = 20

2p - 48 = 20(2)

2p - 48 = 40

2p = 40 + 48

p = 88/2

p = 44

So, the value of p is 44.

Problem 5 :

The vertices are (p, p), (5, 6), (5, –2) and has the area of 32 square units.

Solution :

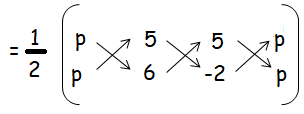
Area of triangle = (1/2) [(6p - 10 + 5p) - (5p + 30 - 2p)]

(1/2) [(6p - 10 + 5p - 5p - 30 + 2p] = 32 square units

(1/2) (8p - 40)  = 32 square units

(8p - 40) = 32(2)

8p - 40 = 64

8p = 64 + 40

8p = 104

p = 104/8

p = 13

So, the value of p is 13.

Problem 6 :

The area of triangle formed by the points (−5,0) , (0,−5) and (5,0) is 

(A) 0 sq.units     (B) 25 sq.units     (C) 5 sq.units

(D) none of these

Solution :

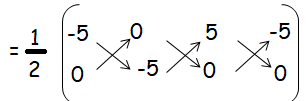
= (1/2) [(25 + 0 + 0) - (0 - 25 - 0)]

= (1/2) [25 - (- 25)]

= (1/2) (25 + 25)

= (1/2) x 50

= 25 square units.

So, the required area of triangle is 25 square units.

Problem 7 :

If (5, 7), (3, p) and (6, 6) are collinear, then the value of p is

(A) 3     (B) 6     (C) 9     (D) 12

Solution :

Since these points are collinear, then the area of triangle joining these three points will be 0.

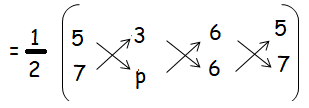
0 = (1/2) [(5p + 18 + 42) - (21 + 6p + 30)]

0 = (1/2) [(5p + 60) - (51 + 6p)]

0 = (1/2) [5p + 60 - 51 - 6p]

0 = (1/2) [-p + 9]

-p + 9 = 0

p = 9

So, the value of p is 9.

In each of the following, find the value of ‘a’ for which the given points are collinear.

Problem 8 :

(2, 3), (4, a) and (6, –3)

Solution :

When the points are collinear, the area created by these points will be 0.

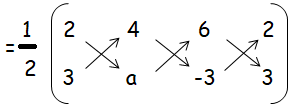
= (1/2)[(2a - 12 + 18) - (12 + 6a - 6)]

= (1/2)[(2a + 6) - (6 + 6a)]

= (1/2)[2a + 6 - 6 - 6a]

= (1/2)[-4a]

4a = 0

a = 0

So, the required value of a is 0.

Problem 9 :

(a, 2 – 2a), (–a + 1, 2a) and (–4 – a, 6 – 2a)

Solution :

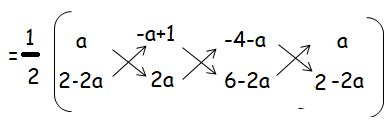
= (1/2){[2a² + (-a + 1)(6 - 2a) + (-4 - a) (2 - 2a)] - [(2 - 2a)(-a + 1) + 2a(-4 - a) + a(6 - 2a)]

= (1/2){ [2a² -6a + 2a² + 6 - 2a - 8 + 8a - 2a + 2a²] - 

[-2a + 2 + 2a²  - 2a - 8a - 2a²  + 6a - 2a²] }

= (1/2){ [6a² - 2a - 2] -  (-2a² - 6a + 2)] }

0 = (1/2){6a² - 2a - 2 + 2a² + 6a - 2}

8a² - 4a - 4 = 0

Dividing by 4, we get

2a² - a - 1 = 0

(2a + 1)(a - 1) = 0

a = -1/2 and a = 1

so, the possible values of a are 1 and -1/2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.