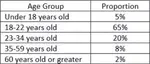
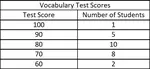
FINDING UNIT RATES

Problem 1 : 

While remodeling her kitchen, Angela is repainting. She estimates that she paints 55 square feet every half-hour. How many square feet does Angela paint per hour?

Solution :

Step 1 : 

Determine the units of the rate.

The rate is area in square feet per time in hours.

Step 2 : 

Find Angela’s rate of painting in area painted per time.

Area painted : 55 sq ft and Time : 1/2 hour

Area painted/Time  =  (55 square ft)/(1/2 hour)

The fraction represents area in square feet per time in hours.

Step 3 : 

Find Angela’s unit rate of painting in square feet per hour.

Rewrite the fraction as division :

(55 square ft)/(1/2 hour)  =  55 ÷ 1/2

Multiply by the reciprocal :

=  55 x 2/1

=  110 square feet/1 hour

(The unit rate has a denominator of 1)

Angela paints 110 square feet per hour.

Problem 2 : 

Paige mows 1/6 acre in 1/4 hour. How many acres does Paige mow per hour?

Solution :

Step 1 : 

Determine the units of the rate.

The rate is area in acre per time in hours.

Step 2 : 

Find Paige's rate of mowing in area mowed per time.

Area mowed : 1/6 acre and Time : 1/4 hour

Area mowed/Time  =  (1/6 acre)/(1/4 hour)

The fraction represents area in acre per time in hours.

Step 3 : 

Find Paige’s unit rate of mowing in acre per hour.

Rewrite the fraction as division :

(1/6 acre)/(1/4 hour)  =  1/6 ÷ 1/4

Multiply by the reciprocal :

=  (1/6) x 4/1

=  (4/6)/1

=  2/3 acre/1 hour

(The unit rate has a denominator of 1)

Paige mows 2/3 of an acre per hour. 

Problem 3 : 

Greta uses 3 ounces of pasta for every 3/4 cup of sauce. How much pasta does she use per cup of sauce ?

Solution :

Step 1 : 

Determine the units of the rate. The rate is in ounces per cup.

Step 2 : 

Find Greta's rate of using pasta in ounces per cup of sauce. 

Pasta used : 3 ounces and Sauce : 3/4 cups

Pasta used/Sauce  =  3 ounces/(3/4 cups)

The fraction represents pasta in ounces per 3/4 cup of sauce.

Step 3 : 

Rewrite the fraction as division :

 3 ounces/(3/4 cups) = 3 ÷ 3/4

Multiply by the reciprocal :

=  3 x 4/3

=  4/1

=  4 ounces/1 cup

(The unit rate has a denominator of 1)

Greta uses 4 ounces of pasta for every 1 cup of sauce.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.