FINDING THE VOLUME OF A SPHERE IN A REAL WORLD CONTEXT

We can find the volume of a sphere using the volume of a cylinder.

Cylinder is a solid which has a circular base.

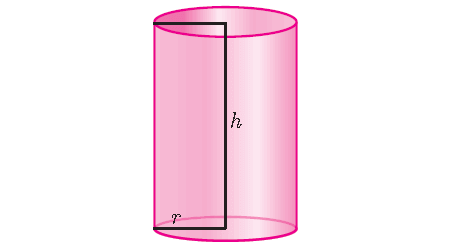
We know the fact that the volume of any solid is equal to the product of base area and height of the solid.

So, the volume of a right circular cylinder of base radius ‘r’ and height ‘h’ is given by

V = (Base Area) x (Height)

The base of a cylinder is a circle, so for a cylinder,

Base Area = πr²

Therefore,

Volume of a cylinder = πr²h cubic units

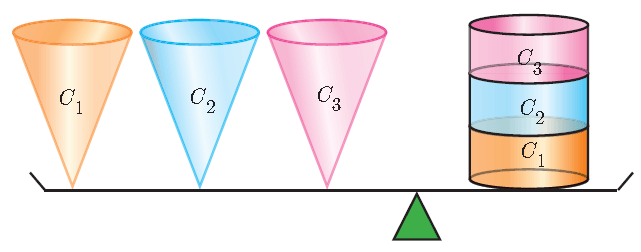
Consider a right circular cylinder and three right circular cones of same base radius and height as that of the cylinder.

The contents of three cones will exactly occupy the cylinder.

Then,

When we model the volume of a sphere, we will be getting the following result.

3 x (Volume of a cone) = Volume of cylinder

3 x (Volume of a cone) = πr²h

Volume of the cone = 1/3 · πr²h cubic units

Consider a sphere and two right circular cones of same base radius and height such that twice the radius of the sphere is equal to the height of the cones.

Then we can observe that the contents of two cones will exactly occupy the sphere.

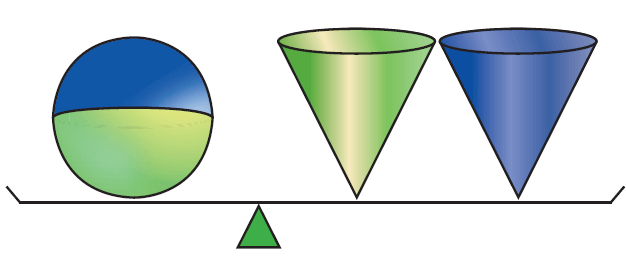
Then,

Volume of sphere  = 2 x (Volume of a cone)

Volume of a sphere = 2 x (1/3 · πr²h)

Volume of a sphere = 2/3 · πr²h

A sphere always has a height which is equal to twice the radius.

So, substitute 2r for h.

Volume of sphere = 2/3 · πr²(2r)

Simplify.

Volume of sphere = 4/3 · πr³ cubic units

Example 1 :

Soccer balls come in several different sizes. One of the soccer balls has a diameter of 24 centimeters. What is the volume of this soccer ball ? Round your answer to the nearest tenth. Use the approximate of value of  ∏, that is 3.14.

Solution :

Step 1 :

Because soccer ball is in the shape of sphere, we can use the formula of volume of a sphere to find volume of the soccer ball.

Write the formula to find volume of a sphere.

V = 4/3 · πr³ ----(1)

Step 2 :

To find the volume, we need the radius of the sphere. But, the diameter is given, that is  24 cm. So, find the radius.

r = diameter/2

r = 24/2

r = 12

Step 3 :

Substitute π ≈ 3.14 and r = 12 in (1).

V ≈ 4/3 · 3.14 · 12³

Simplify.

V ≈ 4/3 · 3.14 · 1728

V ≈ 7,234.6

So, the volume of the soccer ball is about 7,234.6 cubic cm.

Example 2 :

Jose measures the diameter of a ball as 14 inches. How many cubic inches of air can the ball hold, to the nearest tenth ? Use the approximate of value of  ∏, that is 3.14.

Solution :

Step 1 :

To know how much air the ball can hold, we have to find the volume of the ball.

Because a ball is in the shape of sphere, we can use the formula of volume of a sphere to find volume of a ball.

Write the formula to find volume of a sphere.

V = 4/3 · πr³ ----(1)

To find the volume, we need the radius of the sphere. But, the diameter is given, that is  14 cm. So, find the radius.

r = diameter/2

r = 14/2

r = 7

Step 3 :

Substitute π ≈  3.14 and r = 7 in (1).

V ≈ 4/3 · 3.14 · 7³

Simplify.

V ≈ 4/3 · 3.14 · 343

V ≈ 1,436

So, the ball can hold about 1,436 cubic inches.

Example 3 :

Air is leaking from a spherical-shaped advertising balloon at the rate of 26 cubic feet per minute. If the radius of the ball is 7 feet, how long would it take for the balloon to empty fully ? Round your answer to the nearest minute. Use the approximate of value of π, that is 3.14.

Solution :

Step 1 :

To know how long it would take for the balloon to empty fully, first we have to find the volume of air in the balloon.

Because the balloon is in the shape of sphere, we can use the formula of volume of a sphere to find volume of air in the balloon.

Write the formula to find volume of a sphere.

V = 4/3 · πr³ ----(1)

Step 2 :

Substitute π ≈ 3.14 and r = 7 in (1).

V ≈ 4/3 · 3.14 · 7³

Simplify.

V ≈ 4/3 · 3.14 · 343

V ≈ 1,436

So, the volume of air in the balloon is about 1,436 feet.

Step 3 :

Air is leaking from the balloon at the rate of 26 cubic feet per minute.

To know how long it would take for the balloon  to empty 1,426 cubic feet of air, divide 1,426 by 26.

= 1,426 / 26

= 54.8

  ≈ 55

So, it would take about 55 minutes for the balloon to empty fully.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.