FINDING THE SURFACE AREA OF A COMPOSITE SOLID

A composite solid is made up of two or more solid figures.

To find the surface area of a composite solid, find the surface area of each figure. Subtract any area not on the surface.

Example 1 : 

Daniel built the birdhouse shown below. What was the surface area of the birdhouse before the hole was drilled ?

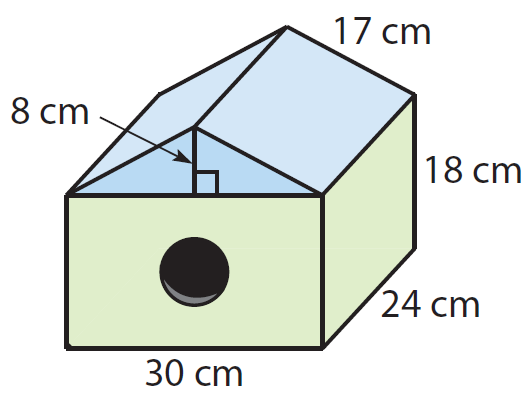
Solution : 

Step 1 :

Identify the important information.

• The top is a triangular prism with h = 24 cm. The base is a triangle with height 8 cm and base 30 cm.

• The bottom is a rectangular prism with h = 18 cm. The base is a 30 cm by 24 cm rectangle.

• One face of each prism is not on the surface of the figure.

Step 2 : 

Find the surface area of each prism.

Add the areas. Subtract the areas of the parts not on the surface.

Step 3 : 

Find the area of the triangular prism.

Perimeter  =  17 + 17 + 30  =  64 cm

Base area  =  (1/2)(30)(8)  =  120 sq.cm

Surface area  =  Ph + 2B

Surface area  =  64(24) + 2(120)

Surface area  =  1,776 sq.cm

Step 4 : 

Find the area of the rectangular prism.

Perimeter  =  2(30) + 2(24)  =  108 cm

Base area  =  30(24)  =  720 sq.cm

Surface area  =  Ph + 2B

Surface area  =  108(18) + 2(720)

Surface area  =  3,384 sq.cm

Step 5 : 

Add. Then subtract twice the areas of the parts not on the surface.

Surface area  =  1,776 + 3,384 - 2(720)  =  3,720 sq.cm

The surface area before the hole was drilled was 3,720 sq.cm.

Example 2 : 

Dara is building a plant stand. She wants to stain the plant stand, except for the bottom of the larger prism. Find the surface area of the part of the plant stand she will stain.

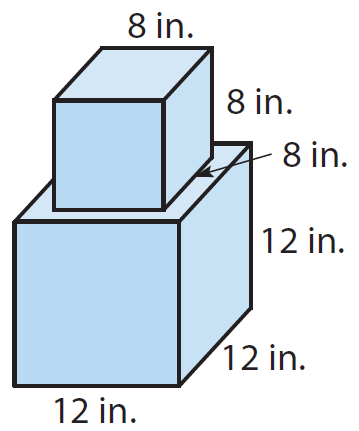
Solution : 

Step 1 :

Identify the important information.

• The top is a  cube with side length of 8 in. 

• The bottom is a cube with side length of 12 in. 

Step 2 : 

Find the surface area of each prism.

Add the areas. Subtract the areas of the parts not on the surface.

Step 3 : 

Find the surface area of the cube which is at the top. 

Surface area  =  6a²

Surface area  =  6(8)²

Surface area  =  6(64)

Surface area  =  384 sq.in

Step 4 : 

Find the surface area of the cube which is at the bottom. 

Surface area  =  6a²

Surface area  =  6(12)²

Surface area  =  6(144)

Surface area  =  864 sq.in

Step 5 : 

Add. Then subtract the areas of the two parts not on the surface.

Required surface area is 

=  384 + 864 - 144 - 64 - 64 

=  976 sq.in

The surface area of the part of the plant stand she will stain is 976 sq.in.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.