FINDING THE RADIUS FROM CIRCUMFERENCE WORKSHEET

Questions 1-2 : Find the missing length in the circle.

In all the questions, use π = 3.14, if required.

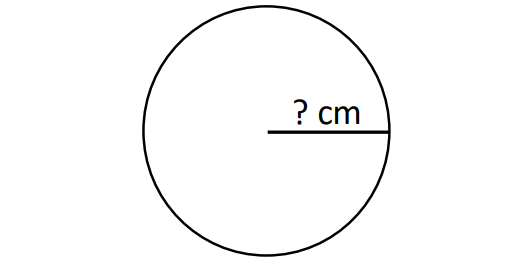
Question 1 :

Solution :

The missing length in the above circle is radius.

Given : Circumference = 16π in.

2πr = 16π

Divide both sides by 2π.

r = 8

Radius = 8 in.

Question 2 :

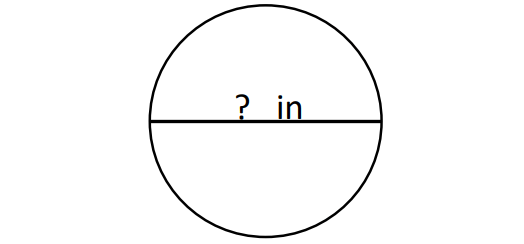
Solution :

The missing length in the above circle is diameter.

Given : Circumference = 75.36 in.

2πr = 75.36

Substitute π = 3.14.

2(3.14)r = 75.36

6.28r = 75.36

Divide both sides by 6.28.

r = 12 in.

Diameter = 2 x Radius

= 2 x 12

= 24 in.

Question 3 :

A circular pond has a circumference of 628 feet. A model boat is moving directly across the pond, along a radius, at a rate of 5 feet per second. How long does it take the boat to get from the edge of the pond to the center ?

Solution :

Step 1 :

Find the radius of the pond.

Circumference = 628

2πr = 628

Substitute π = 3.14.

2(3.14)r = 628

6.28r = 628

Divide both sides by 6.28.

r = 100

Radius = 100 feet

Step 2 :

Find the time taken by the boat to get from the edge of the pond to the center along the radius.

Time = Distance/ Speed

= 100/5

= 20

Hence, the boat takes 20 seconds to get from the edge of the pond to the center.

Question 4 :

The circumference of a car wheel is 62.8 inches. Find its diameter.

Solution :

Diameter = 2 x Radius 

Step 1 :

Find the radius of the wheel.

Use the circumference formula. 

Circumference = 62.8

2πr = 62.8

Substitute π = 3.14.

2(3.14)r = 62.8

6.28r = 62.8

Divide both sides by 6.28.

r = 10

Radius = 10 in.

Step 2 :

Diameter = 2 x Radius

= 2 x 10 in.

= 20 in

Hence, diameter of the car wheel is 20 inches. 

Question 5 :

The Ferris wheel can travel 2376 feet in one ride. If there are 12 revolutions in one ride, find the diameter of the wheel.

Solution :

Diameter = 2 x Radius

Step 1 :

Find the radius of the wheel.

1 ride = 2260.8 feet

12 revolutions = 2260.8 feet.

Divide both sides by 12.

1 revolution = 188.4 feet

Distance traveled in 1 revolution is equal to circumference of the Ferris wheel.

Circumference = 188.4

2πr = 188.4

Substitute π = 3.14.

2(3.14)r = 188.4

6.28r = 188.4

Divide both sides by 6.28.

r = 60

Radius = 60 feet

Step 2 :

Diameter = 2 x Radius

= 2 x 60 feet

= 60 feet

Hence, diameter of the Ferris wheel is 60 feet.

Question 6 :

Find the circumference of a circle whose area is 1256 cm². (π ≈ 3.14)

Solution :

Area of the circle = 1256 cm²

π ≈ 3.14

πr² = 1256

3.14r² = 1256

r² = 1256/3.14

r² = 400

r = 20

Finding circumference :

= 2πr

= 2 x 3.14 x 20

= 125.6 cm

Question 7 :

Find the ratio of the areas of two circles whose circumferences are in the ratio 3 : 2.

Solution :

Ratio between circumference = 3 : 2

Let r₁ and r₂ be radii of circles.

2πr₁ : 2πr₂ = 3 : 2

r₁ : r₂ = 3 : 2

r₁ = 3r₂/2

Ratio between areas = πr₁² : πr₁²

= (3r₂/2)² / r_2²

= 9/4

So, the required ratio between area of two circles is 9 : 4.

Question 8 :

A car’s tyre makes 1000 rotations to cover 1.256 km. Find the diameter of the tyre. (π ≈ 3.14)

Solution :

1000 rotations covers the distance of 1.256 km

1 rotation will cover = 1.256/1000

= 0.001256 km

2πr = 0.001256

2 x 3.14 x r = 0.001256

r = 0.001256/6.28

r = 0.0002

Diameter = 0.0004 km

Converting into m, 

= 0.0004 x 1000

= 4 m is the required diameter of the tyre.

Question 9 :

A circular track has a radius of 200 m. A girl completes seven rounds of the track in two hours. What was her average speed?  (π = 22/7)

Solution :

Radius of circular track = 200 m

Distance covered in 1 round = 2πr

= 2 x (22/7) x 200

Rounding the track 7 times, then the distance covered in 7 rounds

= 7 x 2 x (22/7) x 200

= 8800 m

Average speed = total distance covered / total time taken

= 8800/2 hours

= 4400 meter per hour

1 hour = 60 minutes

1 minute = 60 seconds

= 4400/3600

= 1.22 meter per second.

Question 10 :

The radius of a circle was increased, due to which the circle’s area doubled. By what factor was the radius increased?

Solution :

Radius of the circle = r

Radius of circle after increasing radius = R

πR² = 2πr²

R² = 2r²

R = √2r²

R = √2r

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.