FINDING THE HCF OF ALGEBRAIC EXPRESSIONS WORKSHEET

Find the HCF of the following :

(1)  4x and 12

(2)  3x and 6

(3)  3ab and 6b

(4)  4y and 4xy

(5)  6x² and 2x

(6)  3y and 9y²

(7)  2(x – 1) and 3(x – 1)

(8)  4(x + 2) and (x + 2)

(9)  3(x + 1) and (x + 1) (x – 4)

(10)  (x - 2)² and 2(x - 2) (x – 5)

(11)  2x(5 - x) and x²(5 - x)

(12)  (x + 2)² and 5(x - 4) (x + 2)

Solution

Find the highest common factor of the following :

(i)  c² - d², c(c - d)

(ii)  x⁴ - 27a³x, (x - 3a)²

(iii)  m² - 3m - 18,  m² + 5m + 6

(iv)  x² + 14x + 33, x³ + 10x² - 11x

(v)  x² + 3x y + 2y², x² + 5xy + 6y²

(vi)  2x² - x - 1, 4x² + 8x + 3

(vii)  x² - x - 2, x² + x - 6, 3x² - 13x + 14

(viii)  x³ - x² + x - 1, x⁴ - 1

(ix)  24 (6x⁴ - x³ - 2x²), 20(2x⁶ + 3x⁵ + x⁴)

(x)  (a - 1)⁵ (a + 3)², (a - 2)² (a - 1)³ (a + 3)⁴

Solution

Question 1 :

Find the HCF of the following pairs of polynomials using division algorithm

x³ - 9 x² + 23 x - 15 ,  4 x² - 16 x + 12

Solution

Question 2 :

Find the HCF of the following pairs of polynomials using division algorithm

3 x³ + 18 x² + 33 x + 18 ,  3 x² + 13 x + 10

Solution

Question 3 :

Find the HCF of the following pairs of polynomials using division algorithm

2 x³ + 2 x² + 2 x + 2 ,  6 x³ + 12 x² + 6 x + 12

Solution

Question 4 :

Find the HCF of the following pairs of polynomials using division algorithm

x³ - 3 x² + 4 x - 12 , x⁴ + x³ + 4 x² + 4 x

Solution

Question 1 :

Find the least common multiple of

xy(k² + 1) + k(x² + y²) and xy(k² − 1) + k(x² − y²)

Solution

Question 2 :

Find the GCD of the following by division algorithm

2x⁴ + 13x³ + 27x² + 23x + 7 , x³ + 3x² + 3x + 1 , x² + 2x + 1

Solution

Question 3 :

Reduce the given Rational expressions to its lowest form

(i)  (x^3a - 8)/(x^2a + 2x^a + 4)

(ii)  (10x³ - 25x² + 4x - 10)/(-4 - 10x²)

Solution

Question 4 :

Simplify 

Solution

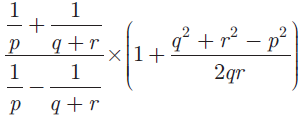
Question 5 :

Arul, Ravi and Ram working together can clean a store in 6 hours. Working alone, Ravi takes twice as long to clean the store as Arul does. Ram needs three times as long as Arul does. How long would it take each if they are working alone?

Solution

Problem 1 : 

Find the GCD of the following polynomials.

x⁴ + 3x³ − x − 3, x³ + x² − 5x + 3

Solution

Problem 2 :

Find the GCD of the following polynomials.

x⁴  - 1,  x³ - 11x² + x - 11

Solution

Problem 3 :

Find the GCD of the following polynomials.

3x⁴ + 6x³ − 12x² − 24x, 4x⁴  + 14x³ + 8x² − 8x

Solution

Problem 4 :

Find the GCD of the following polynomials.

3x³ + 3x² + 3x + 3 , 6x³ + 12x² + 6x + 12

Solution

Problem 5 :

Find the HCF and LCM of the expressions x² - 5x + 6 and x² - 7x + 10 by factorization.

Solution

Problem 6 :

Find the HCF and LCM of the expressions (x + 3) (6x² + 5x - 4) and (2x² + 7x + 3)(x + 3) by factorization.

Solution

Problem 7 :

Find the HCF and LCM of the expressions 

(x² + xy + y²) and (x³ - y³)

Solution

Problem 8 :

Find the HCF and LCM of the expressions 

(x² - 9) and (x² - 6x + 9)

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.