FINDING THE AREA OF A COMPOSITE FIGURE

Example 1 :

Find the area of the figure given below.

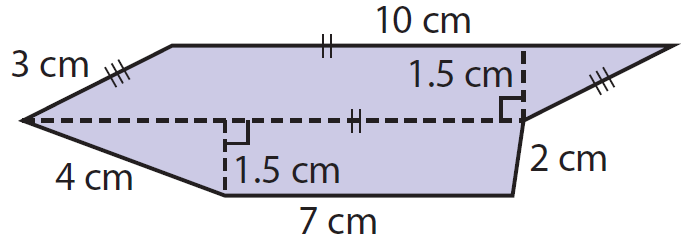
Solution :

Step 1 :

Separate the figure into smaller, familiar figures: a parallelogram and a trapezoid.

Step 2 :

Find the area the parallelogram.

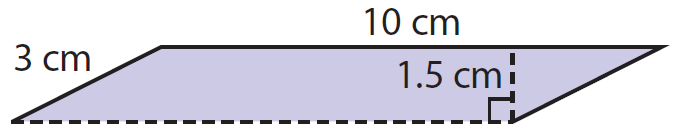
Base (b) = 10 cm

Height (h) = 1.5 cm

Use the formula.

A = bh

A = 10 · 1.5

= 15

The area of the parallelogram is 15 square cm.

Step 3 :

Find the area the trapezoid.

Base₁ (b₁) = 7 cm

Base₂ (b₂) = 10 cm

Height (h) = 1.5 cm

Use the formula.

A = (1/2)h(b₁ + b₂)

= (1/2)(1.5)(7 + 10)

= (1/2)(1.5)(17)

= 12.75

The area of the trapezoid is 12.75 square cm.

Step 4 :

Add the areas to find the total area.

A = 15 + 12.75

= 27.75

So, the area of the given composite figure is 27.75.

Example 2 :

Find the area of the figure given below.

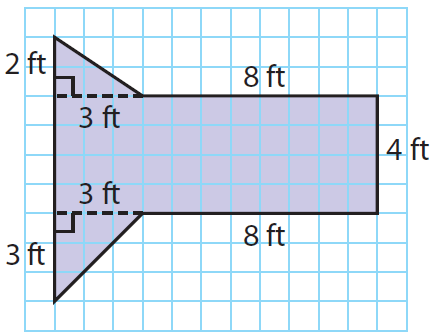
Solution :

Step 1 :

Separate the figure into smaller, familiar figures: a two triangles and a rectangle.

Step 2 :

Find the area the first triangle.

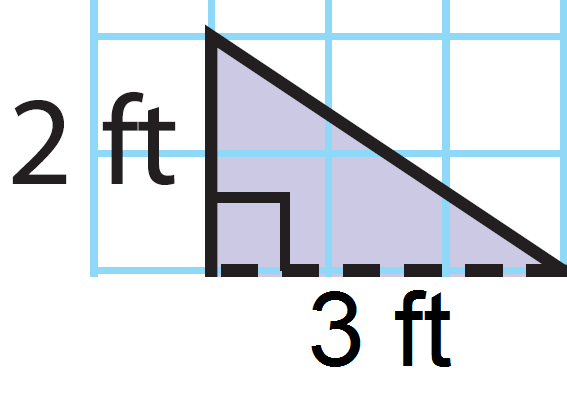
Base (b) = 3 ft

Height (h) = 2 ft

Use the formula.

A = (1/2)bh

= (1/2)(3)(2)

= 3

The area of the first triangle is 3 square ft.

Step 3 :

Find the area the rectangle.

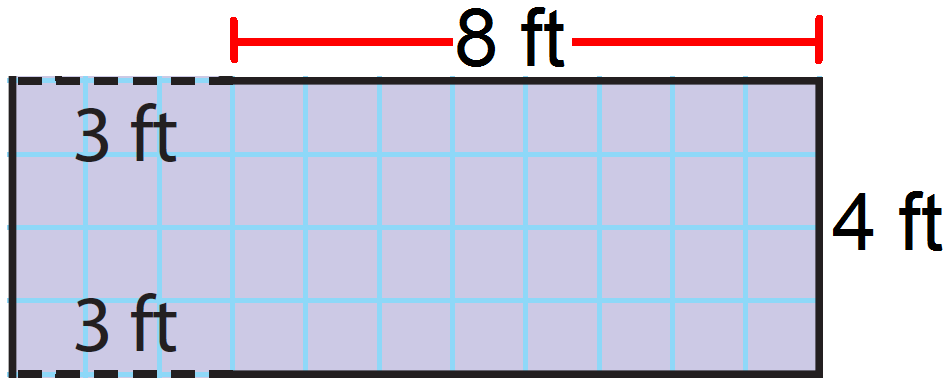
Length (l) = 8 + 3  =  11 ft

Height (h) = 4 ft

Use the formula.

A = l x w

= 11 x 4

= 44

The area of the rectangle is 44 square ft.

Step 4 :

Find the area the second triangle.

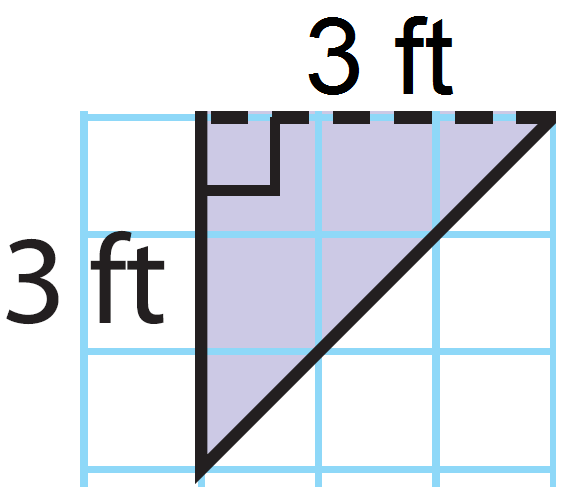
Base (b) = 3 ft

Height (h) = 3 ft

Use the formula.

A = (1/2)bh

= (1/2)(3)(3)

= 4.5

The area of the second triangle is 4.5 square ft.

Step 5 :

Add the areas to find the total area.

A = 3 + 44 + 4.5

= 51.5

So, the area of the given composite figure is 51.5 square feet.

Example 3 :

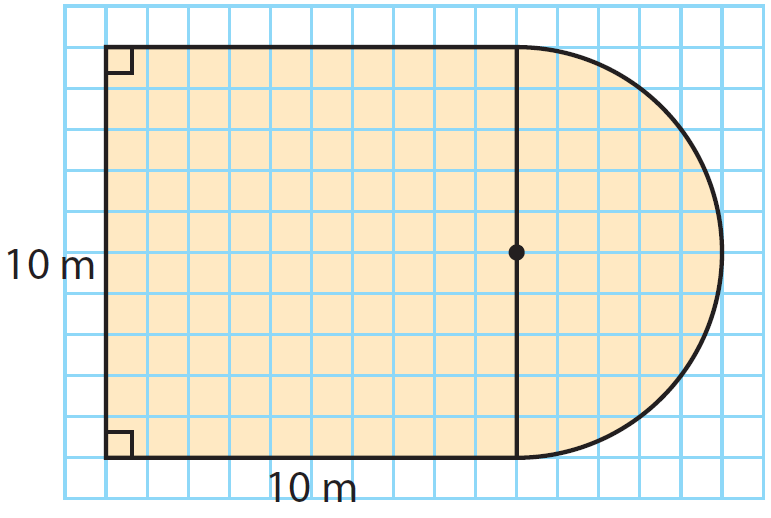
Find the area of the figure given below.

Solution :

Step 1 :

Separate the figure into smaller, familiar figures: a square and a semicircle.

Step 2 :

Find the area the square.

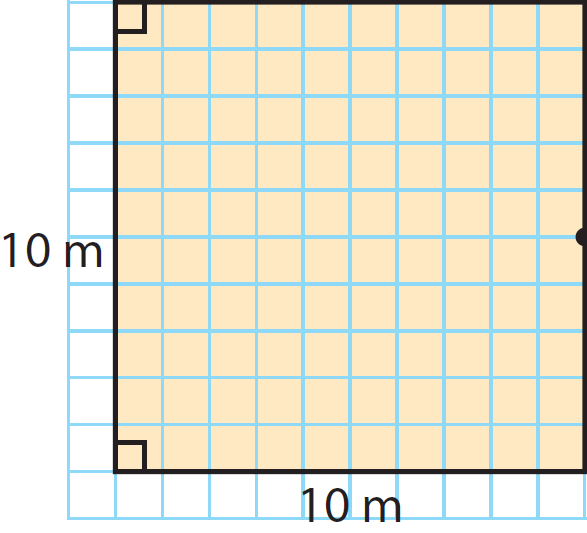
Length of each side = 10 m

Use the formula.

A = Side x Side

= 10 x 10

= 100

The area of the rectangle is 100 square meter.

Step 3 :

Find the area the semicircle.

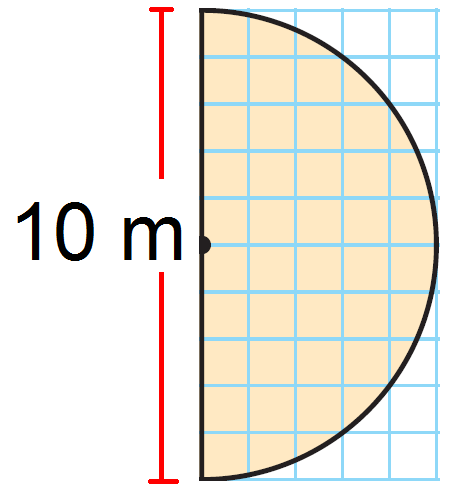
Diameter = 10 m

Radius (r) = Diameter/2

= 10/2

= 5 m

Use the formula.

A = (1/2)πr²

= (1/2)(3.14)(5)²

= 1.57 x 25

= 39.25

The area of the semi circle is about 39.25 square meter.

Step 4 :

Add the areas to find the total area.

A = 100 + 39.25

= 139.25

So, the area of the given composite figure is about 139.25 square meter.

Example 4 :

Find the area of the composite figure.

Solution :

Area of composite figure = area of kite + area of parallelogram

Area of kite = (1/2) x d₁ x d₂

Area of parallelogram = base x height

Area of kite = (1/2) x 6 x 9

= 27 square feet

Area of parallelogram = 4 x (9 - 6)

= 4 x 3

= 12 square feet

Area of composite figure = 27 + 12

= 39 square feet

Example 5 :

Solution :

Area of composite figure = area of sector + area of equilateral triangle

= (θ/360)πr² + (√3/4)a²

= (74/360) x 3.14 x 10² + (√3/4) x 10²

= 0.205 x 3.14 x 100 + (1.732/4) x 100

= 64.54 + 43.3

= 107.84 square meter

Example 6 :

Solution :

Area of composite figure = area of hexagon + area of trapezium

Side length of hexagon = 9 inches,

Apothem = 7 inches

Parallel sides of trapezium = 15 inches and 9 inches

height = 7 inches

= (1/2) x perimeter x apothem + (1/2) x h x (a + b)

= (1/2) x 6 x 9 x 7 + (1/2) x 7 (15 + 9)

= 3 x 9 x 7 + (1/2) x 7 x 24

= 189 + 84

= 273 square inches

Example 7 :

Solution :

Area of composite figure = area of pentagon + area of rhombus + area of right triangle

= (1/2) x perimeter x apothem + (1/2) x (d₁ + d₂) + (1/2) x base x height

= (1/2) x 6(5) x 5.1 + (1/2) x (10 x 6.6) + (1/2) x 4 x 6

= (3 x 5 x 5.1) + (5 x 6.6) + (2 x 6)

= 76.5 + 33 + 12

= 121.5 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.