FINDING LENGTH OF DIAGONAL OF A RECTANGLE

A rectangle is a special case of a parallelogram in which each pair of adjacent sides is perpendicular. 

Diagonals will divide the rectangle into two right triangles.

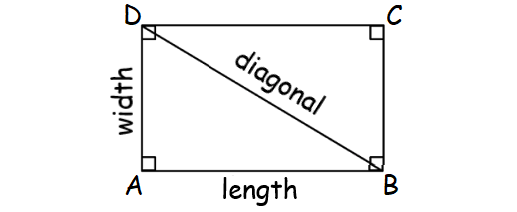
We can find the length of diagonal BD in the rectangle ABCD above using Pythagorean Theorem in the right ΔABD.

In the right ΔABD, by Pythagorean Theorem,

BD² = AB² + AD²

Take square root on both sides.

Example 1 :

A rectangle has sides of length 8 cm and 3 cm. Find the length of each diagonal.

Solution :

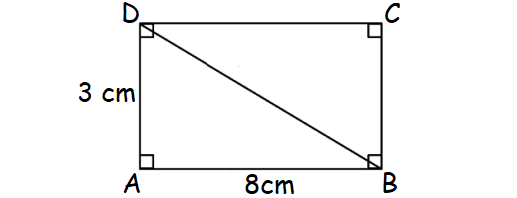
In the rectangle ABCD above, AB = 8 cm and AD = 3 cm.

In the right ΔABD, by Pythagorean Theorem,

BD² = AB² + AD²

BD² = 8² + 3²

BD² = 64 + 9

DB² = 73

Take square root on both sides.

DB = √73

The length of each diagonal is √73 cm.

Example 2 :

The length of a rectangle is three times of its width. If the diagonal is 10 cm long, find the length and width of the rectangle.

Solution :

Let x be width of the rectangle.

Then, the length = 3x

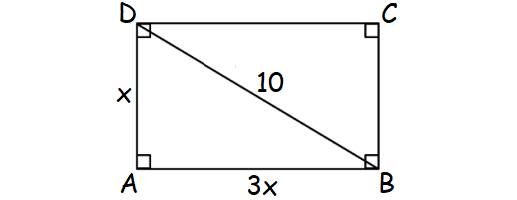
In the right ΔABD, by Pythagorean Theorem,

AB² + AD² = BD²

(3x)² + x² = 10²

9x² + x² = 100

10x² = 100

Divide both sides by 10.

x² = 10

Take square root on both sides.

x = √10

width = √10 cm

length = 3√10 cm

Example 3 :

The length and width of a rectangle are in the ratio 2 : 1. If the diagonal is 10 cm long, find the perimeter and area area of the rectangle.

Solution :

From the ratio 2 : 1, length and width of the rectangle can be assumed as 2x and 1x.

By Pythagorean theorem,

(2x)² + x² = 10²

4x² + x² = 100

5x² = 100

Divide both sides by 5.

x² = 20

Take square root on both sides.

x = √20

x = 2√5

length = 2(2√5) = 4√5

width = 2√5

Perimeter of the rectangle :

= 2(l + w)

= 2(4√5 + 2√5)

= 2(6√5)

= 12√5 cm

Area of the rectangle :

= length x width 

= 4√5(2√5)

= 8(5)

= 40 cm²

Example 4 :

The width of a rectangular field is 60% of its length. If the perimeter of the field is 800 m, find the length of its diagonal (Round your answer to the nearest whole number, if required).

Solution :

Let x be the length.

Then, the width = 60% of x = 0.6x.

Perimeter of the rectangle = 800 m

2(x + 0.6x) = 800

2(1.6x) = 800

3.2x = 800

Divide both sides by 3.2.

x = 250

length = 250 m

width = 0.6(250) = 150 m

By Pythagorean Theorem,

(diagonal)²  =  (length² + (width)²

(diagonal)² = 250² + 150²

(diagonal)² = 625000 + 22500

(diagonal)² = 85000

Take square root on both sides.

diagonal = √85000

diagonal ≈ 292

Length of the diagonal is about 292 m.

Example 5 :

Find the length of the diagonal of a rectangle whose breadth and length are 8 cm and 15 cm respectively.

Solution :

Length = 15 cm, breadth = 8 cm

By using Pythagorean Theorem,

(diagonal)²  =  (length² + (width)²

(diagonal)²  =  15² + 8²

(diagonal)²  = 225 + 64

(diagonal)²  = 289

diagonal = √289

= 17 m

So, the length of diagonal is 17 m.

Example 6 :

ABCD is a rectangle whose diagonals are 2x + 6 and 3x + 4. Find x and the length of the diagonals.

Solution :

In a rectangle, since opposite sides are equal the diagonal will have same length.

2x + 6 = 3x + 4

2x - 3x = 4 - 6

-x = -2

x = 2

So, the value of x is 2.

Applying the value of x in the expressions of length and width, we get

Since the length and width are equal, it must be a square. To find the length of the diagonal, we use Pythagorean theorem.

(diagonal)²  =  (length² + (width)²

(diagonal)²  =  10² + 10²

(diagonal)²  = 100 + 100

diagonal = √200

= √(10 x 10 x 2)

= 10√2

Example 7 :

The width of a rectangle is 20 cm. The diagonal is 8 cm longer than the length. Find the length of the rectangle.

a. 20 cm    b. 23 cm    c. 22 cm   d. 21 cm

Solution :

Width = 20 cm

Let x be the length of the rectangle.

diagonal = x + 8

(diagonal)²  =  (length² + (width)²

(x + 8)²  = x² + 20²

x² + 16x + 64 = x² + 400

16x + 64 = 400

16x = 400 - 64

16x = 336

x = 336/16

x = 21

So, the length of the rectangle is 21 cm. Option d is correct.

Example 8 :

The diagonal of a rectangle is 25 inches. The width is 15 inches. What is the missing length?

Solution :

diagonal = 25 inches, width = 15 inches

(diagonal)²  =  (length² + (width)²

Let x be the length of the rectangle.

25²  = x² + 15²

625 - 225 = x²

400 = x²

x = 20

So, the required length is 20 inches.

Example 9 :

A soccer field is a rectangle 90 meters wide and 120 meters long. The coach asks players to run from one corner to the other corner diagonally across. What is this distance?

Solution :

Width = 90 m, length = 120 m

(diagonal)²  =  length² + (width)²

(diagonal)²  =  120² + 90²

(diagonal)²  =  14400 + 8100

(diagonal)²  = 22500

diagonal = 150 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.