FINDING INTERQUARTILE RANGE WORKSHEET

Problem 1 : 

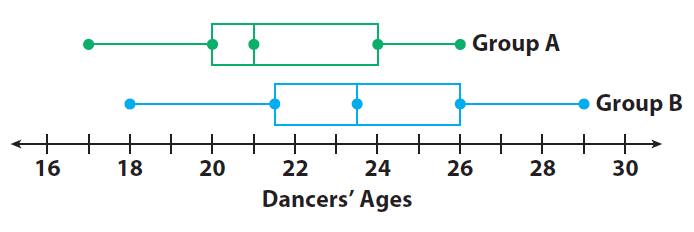
The box plots compare the ages of dancers in two different dance troupes.

(i)  Find the interquartile (IQR) for each set of data.

(ii)  Compare the IQRs. How do the IQRs describe the distribution of the ages in each group ?

Problem 2 :

The box plots compare the weekly earnings of two groups of salespeople from different clothing stores. 

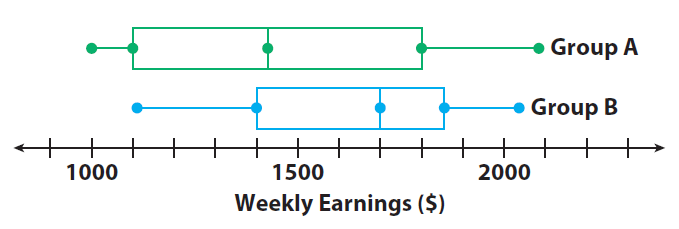
(i)  Find the interquartile (IQR) for each set of data.

(ii)  Compare the IQRs. How do the IQRs describe the data set in each group ?

Problem 3 :

The box plots compare the heights 9 (in inches) of two groups of some small plants. 

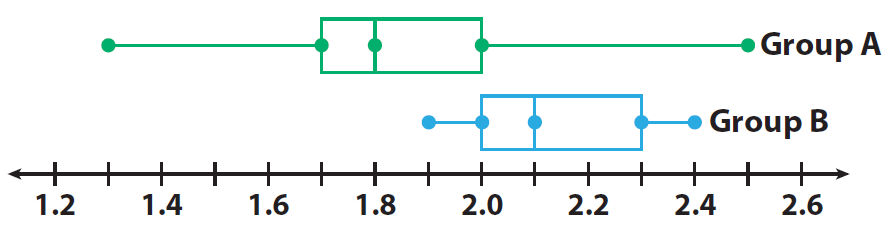
(i)  Find the interquartile (IQR) for each set of data.

(ii)  Compare the IQRs. How do the IQRs describe the data set in each group ?

Detailed Answer Key

Problem 1 :

The box plots compare the ages of dancers in two different dance troupes.

(i)  Find the interquartile (IQR) for each set of data.

(ii)  Compare the IQRs. How do the IQRs describe the distribution of the ages in each group ?

Solution :

Finding the IQR for each set of data :

Group A : IQR  =  Upper quartile − Lower quartile

=  24  − 20

=  4

Group B : IQR  =  Upper quartile − Lower quartile

=  26 − 21.5

=  4.5

Comparing IQRs :

The IQR of group B is slightly greater than the IQR of group A. The ages in the middle half of group B are slightly more spread out than in group A.

Problem 2 :

The box plots compare the weekly earnings of two groups of salespeople from different clothing stores. 

(i)  Find the interquartile (IQR) for each set of data.

(ii)  Compare the IQRs. How do the IQRs describe the data set in each group ?

Solution :

Finding the IQR for each set of data :

Group A : IQR  =  Upper quartile − Lower quartile

=  1800  − 1100

=  700

Group B : IQR  =  Upper quartile − Lower quartile

=  1850 − 1400

=  450

Comparing IQRs :

Group A’s IQR is greater, so the salaries in the middle 50% for group A are more spread out than those for group B.

Problem 3 :

The box plots compare the heights of two groups of some small plants. 

(i)  Find the interquartile (IQR) for each set of data.

(ii)  Compare the IQRs. How do the IQRs describe the data set in each group ?

Solution :

Finding the IQR for each set of data :

Group A : IQR  =  Upper quartile − Lower quartile

=  2.0  − 1.7

=  0.3

Group B : IQR  =  Upper quartile − Lower quartile

=  2.3 − 2.0

=  0.3

Comparing IQRs :

The IQRs are the same. The spreads of the middle 50% of the data values are the same for the two data sets.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.