FINDING EQUATION OF LINE WORKSHEET

Question 1 :

Find the slope of the straight line

(i) 3x + 4y -6 = 0

(ii)  y  =  7x + 6

(iii)  4 x = 5y + 3

Solution

Question 2 :

Show that the straight lines x + 2 y + 1 = 0 and 3x + 6y + 2 = 0 are parallel

Solution

Question 3 :

Show that the straight lines 3x – 5y + 7 = 0 and 15 x + 9y + 4 = 0 are perpendicular.

Solution

Question 4 :

If the straight lines y/2 = x – p and ax + 5 = 3y are parallel, then find a.

Solution

Question 5 :

Find the value of a if the straight lines 5x – 2y – 9 = 0 and ay + 2x – 11 = 0 are perpendicular to each other.

Solution

Question 6 :

• The line Q passes through the points (−10, −2) and (−8, −8)
• The line R passes through the points (1, 2) and (10, a)

The lines Q and R are perpendicular. Find the value of a

Solution

Question 7 :

A line passes through the points (-1, 2) and (5, b) and is parallel to the graph of the equation 4x - 2y = 13, what is the value of b ?

Solution

Question 8 :

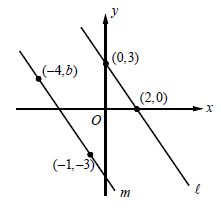
In the xy-plane above, line l is parallel to line m. What is the value of b?

Solution

Question 9 :

In the system of equations above, a and b are constants and x and y are variables. If the system of equations  above has no solution, what is the value of a⋅b?

ax - y = 0

x -  by = 1

Solution

Question 1 :

Find the values of p for which the following two straight lines are perpendicular to each other.

8px + (2 - 3p)y + 1  =  0

px + 8y + 7  =  0

Solution

Question 2 :

If the straight lines passing through the points (h, 3) and (4, 1) intersects the line 7x – 9y – 19 = 0 at right angle, then find the value of h.

Solution

Question 3 :

Given that P = (−1, −1), Q = (4, 3), A = (1, 2), and B = (7, k), find the value of k that makes the line AB

(a) parallel to PQ

(b) perpendicular to PQ

Solution

Question 4 :

Let A = (−6, −4), B = (1, −1), C = (0, −4), and D = (−7, −7). Show that the opposite sides of quadrilateral ABCD are parallel. Such a quadrilateral is called a parallelogram.

Solution

Question 5 :

If the straight lines 12y = -(p + 3)x + 12, 12x -7y = 16 are perpendicular then find p.

Solution

Question 1 :

Find the equation of the straight line which passes through the point of intersection of the straight lines 5x - 6y = 1 and 3x + 2y + 5 = 0 and is perpendicular to the straight line 3x - 5y + 11 = 0.

Solution

Question 2 :

Find the equation of the straight line joining the point of intersection of the lines 3x – y + 9 = 0 and x + 2y = 4 and the point intersection of the lines 2x + y – 4 = 0 and x – 2y + 3 = 0

Solution

Question 3 :

The line joining the points A(0, 5) and B(4, 1) is a tangent to a circle whose centre C is at the point (4, 4) find

(i) the equation of the line AB.

(ii) the equation of the line through C which is perpendicular to the line AB.

(iii) the coordinates of the point of contact of tangent line AB with the circle.

Solution

Question 4 :

Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x - 2y - 4 = 0 to the point of intersection of 7x - 3y = -12 and 2y = x + 3

Solution

Question 1 :

A(-3, 0) B(10, -2) and C(12, 3) are the vertices of 

ΔABC. Find the equations of the altitudes through A, B and C in general form.

Solution

Question 2 :

Write the equation of the perpendicular bisector that goes through the line segment with end points of (9, 5) and (-7, 13).

Solution

Question 3 :

Write the equation of the perpendicular bisector that goes through the line segment with end points of (10, -10) and B (2, 2).

Solution

Question 4 :

Write the equation of the perpendicular bisector that goes through the line segment with end points of (-10, -8) and B (-14 , 8).

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.