EQUATION OF LINE PASSING THROUGH POINT OF INTERSECTION OF TWO LINES

Example 1 :

Find the equation of the straight line which passes through the point of intersection of the straight lines 5x - 6y = 1 and 3x + 2y + 5 = 0 and is perpendicular to the straight line 3x - 5y + 11 = 0.

Solution :

To find the point of intersection of any two lines, we need to solve them

5x - 6y = 1  --(1)

3x + 2y = -5 ----(2)

                       5x - 6y = 1

 (2) x 3 =>   9x + 6y = -15

                 ----------------

                  14 x = -14

                    x = -1

Substitute x = -1 in the first equation

  5 (-1) -6 y = 1

-5 - 6y = 1

-6 y = 1 + 5

-6y = 6

y = -1

Point of intersection of those two lines is (-1,-1)

Slope of the perpendicular line 3x - 5y + 11 = 0

m = -3/(-5)

= 3/5

Slope of the required line = -1/m

= -1/(3/5)

= -5/3

Equation of the line :

(y - y₁) = m (x - x₁)

(y - (-1)) = (-5/3) (x - (-1))

  3 (y + 1) = -5 (x + 1)

 3 y + 3 = - 5 x - 5

 5 x + 3 y + 5 + 3 = 0 

 5 x + 3y + 8 = 0

Example 2 :

Find the equation of the straight line joining the point of intersection of the lines 3x – y + 9 = 0 and x + 2y = 4 and the point intersection of the lines 2x + y – 4 = 0 and x – 2y + 3 = 0

Solution :

To find the point of intersection of any two lines we need to solve them

3x – y + 9 = 0 ---- (1)

x + 2y - 4 = 0 ---- (2)

(1) - (2)

              3x – y + 9 = 0

(2) x 3   3x + 6y - 12 = 0

             (-)  (-)  (+)

           ----------------- 

              - 7y + 21 = 0

                    7y = 21, y = 3

Substitute y = 3 in the first equation

3 x - 3 + 9 = 0

3 x + 6 = 0

3 x = - 6

x = -6/3 = -2 

the point of intersection is (-2, 3)

2x + y – 4 = 0 ---- (3)

x – 2y + 3 = 0 ---- (4)

(1) - (2)

              2x + y - 4 = 0

(2) x 2   2x - 4y + 6 = 0

             (-)    (+)  (-)

           ----------------- 

                  5 y - 10 = 0

                    5y = 10

                     y = 2

Substitute y = 2 in the third equation

2 x + y - 4 = 0

2 x + 2 - 4 = 0

2 x - 2 = 0

2 x = 2

x = 1

the point of intersection is (1, 2)

Equation of the line:

(-2, 3) and (1, 2)

Slope of the line = (2 - 3) / (1 + 2)

= -1/3

(y - y₁) = m(x - x₁)

(y - 3) = -1/3 (x - (-2))

3(y - 3) = -1(x + 2)

3y - 9 = -x - 2

x + 3y = -2 + 9

x + 3y = 7

Example 3 :

The line joining the points A(0, 5) and B(4, 1) is a tangent to a circle whose centre C is at the point (4, 4) find

(i) the equation of the line AB.

(ii) the equation of the line through C which is perpendicular to the line AB.

(iii) the coordinates of the point of contact of tangent line AB with the circle.

Solution :

i)  

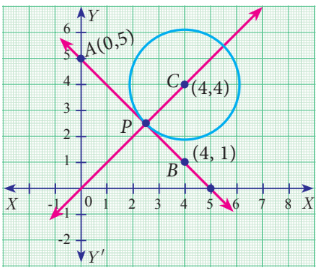
Slope of the line passes through two points A(0, 5) and B(4, 1)

Slope = (1 - 5) / (4 - 0)

= -4/4

= -1

Equation of line :

(y - y₁) = m(x - x₁)

y - 5 = -1(x - 0)

y - 5 = -x

x + y = 5

Equation of the line AB is x + y = 5

ii)

Slope of the line passes through C = -1/(-1)

= 1

Equation of the perpendicular line to AB passes through C:

(y - y₁) = m(x - x₁)

y - 4 = 1(x - 4)

y = x - 4 + 4

y = x

iii)  By finding the point of intersections of x + y = 5 and y = x, we get the required point.

x + x = 5

2x = 5

x = 5/2

Applying the value of x in y = x

y = 5/2.

So, the required point is (5/2, 5/2).

Example 4 :

Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x - 2y - 4 = 0 to the point of intersection of 7x - 3y = -12 and 2y = x + 3

Solution :

3x + y + 2 = 0 ----(1)

x - 2y - 4 = 0 -----(2)

2 (1) + (2)

6x + 2y + 4 = 0

 x - 2y - 4 = 0

----------------

7x + 0 = 0

x = 0

Applying x = 0 in (1), we get

3(0) + y + 2 = 0

y = -2

The point of intersection of these two lines are (0, -2).

7x - 3y = -12------(3)

2y = x + 3

-x + 2y = 3------(4)

(3) + 7(4)

7x - 3y = -12

-7x + 14y = 21

-----------------

11y = 9

y = 9/11

Applying the value of y in (3)

7x - 3(9/11) = -12

7x - (27/11) = -12

7x = -12 + (27/11)

7x = (-132 + 27)/11

7x = -105/11

x = -15/11

The point of intersection of these two points is (-15/11, 9/11)

(0, -2) and (-15/11, 9/11)

Slope of the line = (9/11 + 2) / (-15/11 - 0)

= (9+22)/11 / (-15/11)

= 31/15

Equation of the line :

(y + 2) = 31/15(x - 0)

15(y + 2) = 31x

15y + 30 = 31x

31x - 15y = 30

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.