FINDING DISTANCE IN THE COORDINATE PLANE

We can use absolute values to find distances between two points that have the same x-coordinates or the same y-coordinates on a coordinate plane.

Example 1 :

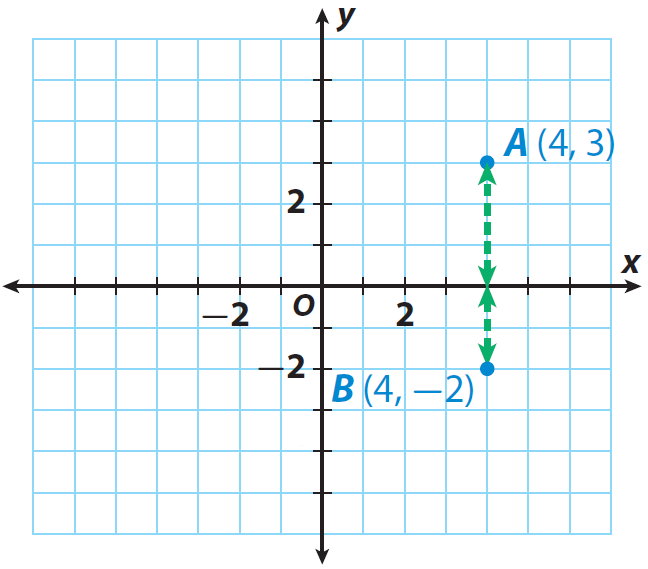
What is the distance between point A(4, 3) and point B(4, -2) ?

Solution :

Step 1 :

Find the distance between point A and the x-axis.

The y-coordinate of A is 3, so point A is |3| = 3 units from the x-axis.

Step 2 :

Find the distance between point B and the x-axis.

The y-coordinate of B is −2, so point B is |−2| = 2 units from the x-axis.

Step 3 :

Find the sum of the distances.

Distance from A to B is

= |3| + |−2| = 3 + 2 = 5 units.

The steps explained above have been illustrated in the graph given below.

Example 2 :

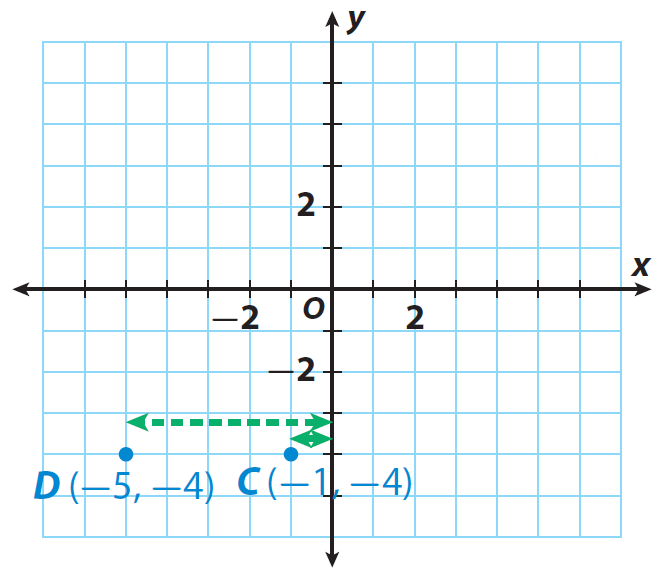
What is the distance between point C(-1, -4) and point D(-5, -4) ?

Solution :

Step 1 :

Find the distance between point C and the y-axis.

The x-coordinate of C is -1, so point C is |-1| = 1 unit from the y-axis.

Step 2 :

Find the distance between point D and the y-axis.

The x-coordinate of D is −5, so point B is |−5| = 5 units from the y-axis.

Step 3 :

Find the distance between C and D by finding this difference :

Distance of D from the y-axis − distance of C from the y-axis

|-5| - |-1| = 5 - 1 = 4 units.

The steps explained above have been illustrated in the graph given below.

Example 3 :

Find the distance between the points A and B in the given graph given below. 

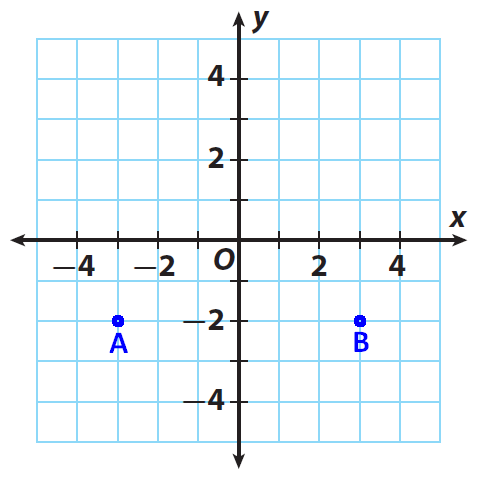
Solution :

From the graph, the ordered pair of A is (-3, -2) and B is (3, -2) respectively. 

Step 1 :

Find the distance between point A and the y-axis.

The x-coordinate of A is -3, so point A is |-3| = 3 units from the y-axis.

Step 2 :

Find the distance between point B and the y-axis.

The x-coordinate of B is 3, so point B is |3| = 3 units from the y-axis.

Step 3 :

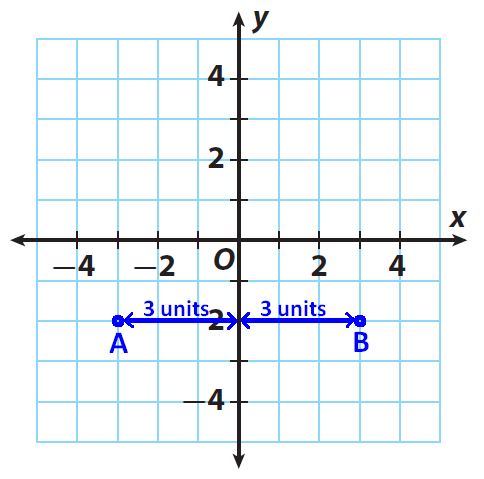
Find the sum of the distances.

Distance from A to B is

= |-3| + |3| = 3 + 3 = 6 units.

The steps explained above have been illustrated in the graph given below.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.