FIND THE LEAST NUMBER SHOULD BE MULTIPLIED TO GET A PERFECT SQUARE

Example 1 :

Find the least number multiplied by 200 to get a perfect square.

Solution :

Decompose 200 into its prime factors.

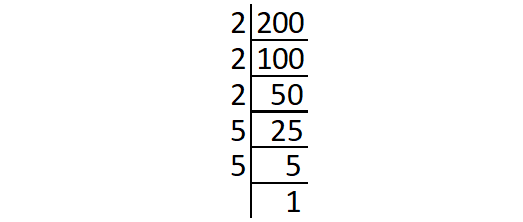
Prime factors of 200 :

200 = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5

= (2 ⋅ 2) ⋅ 2 ⋅ (5 ⋅ 5)

The prime factor 2 does not occur in pair.

So, '2' is the least number to be multiplied by 200 to get a perfect square.

Justification :

√[2(200)] = √[2(2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5)]

√400 = √[(2 ⋅ 2)(2 ⋅ 2)(5 ⋅ 5)]

= 2 ⋅ 2 ⋅ 5

= 20

Further,

2(200) = 400 = 20²

Example 2 :

Find the least number multiplied by 252 to get a perfect square.

Solution :

Decompose 252 into its prime factors.

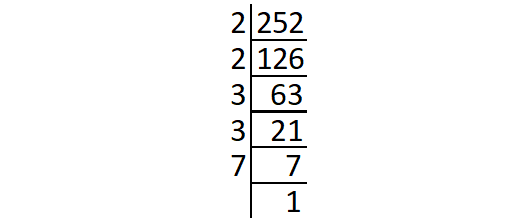
Prime factors of 252 :

252 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 7

= (2 ⋅ 2) ⋅ (3 ⋅ 3) ⋅ 7

The prime factor 7 does not occur in pair.

So, '7' is the least number to be multiplied by 252 to get a perfect square.

Justification :

√[7(252)] = √[7(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 7)]

√1764 = √[(2 ⋅ 2)(3 ⋅ 3)(7 ⋅ 7)]

= 2 ⋅ 3 ⋅ 7

= 42

Further,

7(252) = 1764 = 42²

Example 3 :

Find the least number multiplied by 180 to get a perfect square.

Solution :

Decompose 180 into its prime factors.

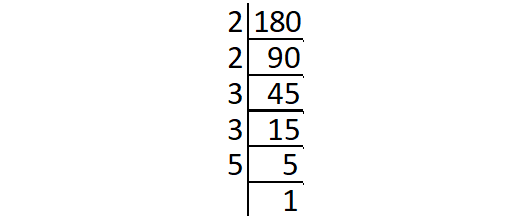
Prime factors of 180 :

180 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5

= (2 ⋅ 2) ⋅ (3 ⋅ 3) ⋅ 5

The prime factor 5 does not occur in pair.

So, '5' is the least number to be multiplied by 180 to get a perfect square.

Justification :

√[5(180)] = √[5(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5)]

√900 = √[(2 ⋅ 2)(3 ⋅ 3)(5 ⋅ 5)]

= 2 ⋅ 3 ⋅ 5

= 30

Further,

5(180) = 900 = 30²

Example 4 :

Find the least number multiplied by 90 to get a perfect square.

Solution :

Decompose 90 into its prime factors.

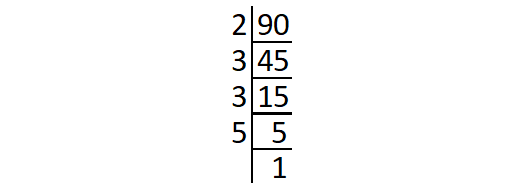
Prime factors of 90 :

90 = 2 ⋅ 3 ⋅ 3 ⋅ 5

= 2 ⋅ (3 ⋅ 3) ⋅ 5

The prime factors 2 and 5 do not occur in pair.

Product of 2 and 5 :

2 ⋅ 5 = 10

So, '10' is the least number to be multiplied by 90 to get a perfect square.

Justification :

√[10(90)] = √[10(2 ⋅ 3 ⋅ 3 ⋅ 5)]

√900 = √[(2 ⋅ 5)(2 ⋅ 3 ⋅ 3 ⋅ 5)]

= √[(2 ⋅ 2)(3 ⋅ 3)(5 ⋅ 5)]

= 2 ⋅ 3 ⋅ 5

= 30

Further,

10(90) = 900 = 30²

Example 5 :

Find the least number multiplied by 120 to get a perfect square.

Solution :

Decompose 120 into its prime factors.

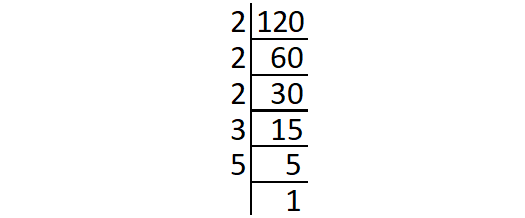
Prime factors of 120 :

120 = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5

= (2 ⋅ 2) ⋅ 2 ⋅ 3 ⋅ 5

The prime factors 2, 3 and 5 do not occur in pair.

Product of 2, 3 and 5 :

2 ⋅ 3 ⋅ 5 = 30

So, '30' is the least number to be multiplied by 120 to get a perfect square.

Justification :

√[30(120)] = √[30(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5)]

√3600 = √[(2 ⋅ 3 ⋅ 5)(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5)]

= √[(2 ⋅ 2)(2 ⋅ 2)(3 ⋅ 3)(5 ⋅ 5)]

= 2 ⋅ 2 ⋅ 3 ⋅ 5

= 60

Further,

30(120) = 3600 = 60²

Example 6 :

The least number by which 294 must be multiplied to make it a perfect square is

a)  2     b)  3    c)  6     d)  24

Solution :

Finding the prime factorization of 294.

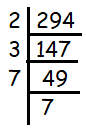
294 = 2 x 3 x 7 x 7

Here we see pair for 7, there is no pair for 2 and 3.

294 = (2 x 2 x 3 x 3 x 7 x 7)

So, the required number to be multiplied to make it as perfect square is 6.

Example 7 :

The least number by which 5808 must be multiplied to make it a perfect square is

a)  2     b)  3    c)  7     d)  11

Solution :

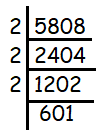
5808 = 2 x 2 x 2 x 601

By inserting one more 2, we may see the pairs. So, 2 is the number should be multiplied to make it as perfect square.

Example 8 :

A man plants 15376 apple trees in his garden and arranges them so that there are as many rows as there are apples trees in each row. The number of rows is 

a)  124     b)  126    c)  134     d)  144

Solution :

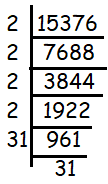
√15376 = √(2 x 2 x 2 x 2 x 31 x 31)

= 2 x 2 x 31

= 124

Number of rows and columns are 124. So, option a is correct.

Example 9 :

Is 2352 a perfect square ? If not find the smallest multiple of 2352 which is a perfect square. Find the square root of the new number.

Solution :

Finding the prime factorization of 2352.

2352 = 2 x 2 x 2 x 2 x 3 x 7 x 7

Since we dont see pair of all numbers, it is not a perfect square.

By inserting 3 we make it as pairs. So, the required number to be multiplied to make it as perfect square is 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.