FIND THE AREA OF THE REGION ENCLOSED BY THE GIVEN CURVES
Example 1 :
Find the area of the region described.
The region bounded by y = 4(x + 1), y = 5(x + 1) and x = 3
Solution :
x-intercepts and y-intercepts of y = 4(x + 1)
|
x-intercept y = 0 x + 1 = 0 x = -1 (-1, 0) |
y-intercept x = 0 y = 4(0 + 1) y = 4 (0, 4) |
x-intercepts and y-intercepts of y = 5(x + 1)
|
x-intercept y = 0 x + 1 = 0 x = -1 (-1, 0) |
y-intercept x = 0 y = 5(0 + 1) y = 5 (0, 5) |
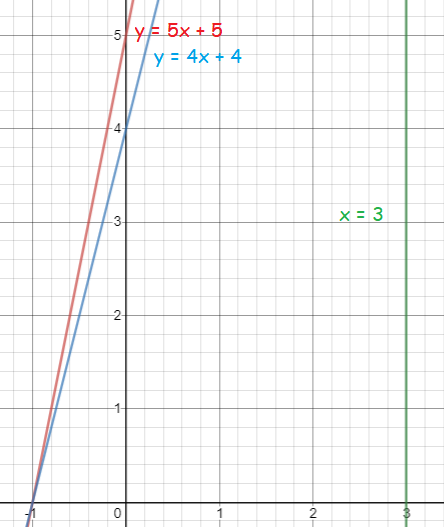
Required area :
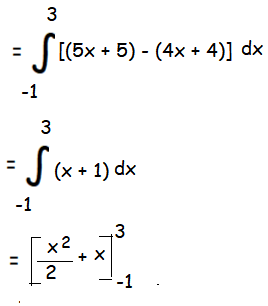
= (9/2 + 3) - (1/2 - 1)
= (15/2) - (-1/2)
= (15 + 1)/2
= 16/2
= 8
Example 2 :
Find the area of the region in the first quadrant bounded by the line y = 2x, the line x = 4 the curve y = 2/x, and the x-axis.
Solution :
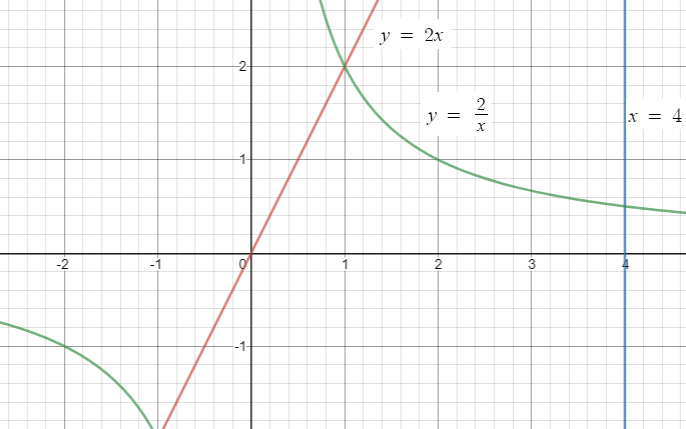
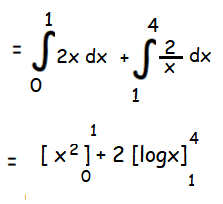
= (1 - 0) + 2(log 4 - log 1)
= 1 + 2 (log4 - 0)
= 1 + log 16
Example 3 :
Find the area of the region bounded by y = √(2x), y = 2x - 2 and y = 0.
Solution :
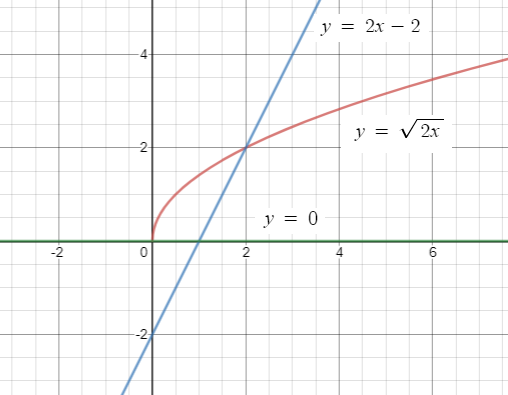
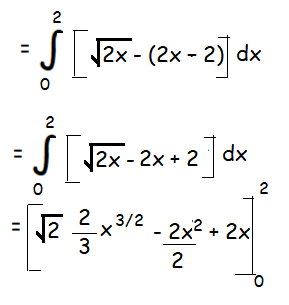
= (2√2/3) (2)3/2 - 4 + 4
= 8/3
So, the required area is 8/3.
Apart from the stuff given on, if you need any other stuff in math, please use our google custom search here.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Subtraction Word Problems Worksheet
Jul 14, 20 07:40 PM
Subtraction Word Problems Worksheet
-
Subtraction Word Problems
Jul 14, 20 07:38 PM
Subtraction Word Problems with Step by Step Explanation
-
Addition Word Problems
Jul 13, 20 10:38 PM
Addition Word Problems
