FIND MACLAURIN EXPANSION

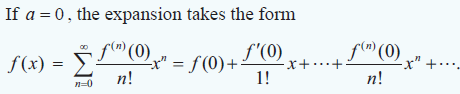
Taylor’s series and Maclaurin's series expansion of a function which are infinitely differentiable

(i)  e^x

Solution :

Let f(x)  =  e^x

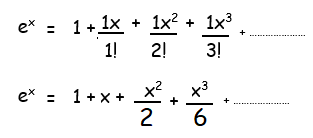
(ii)  sin x

Solution :

Let f(x)  =  sin x

f^v(x)  =  cos x

f^v(0)  =  cos (0)

f^v(0)  =  1

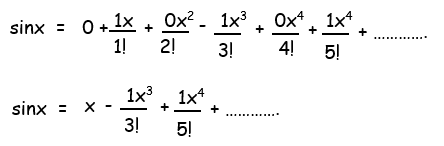
(iii)  cos x

Solution :

Let f(x)  =  cos x

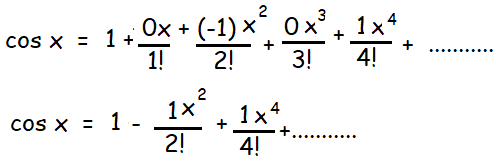
(iv)  log (1-x) ; -1 ≤ x < 1

Solution :

f(x)  =  log (1-x)

f(0)  =  log (1-0)  ==>  0

f'(x)  =  -1/(1-x)

f'(0)  =  -1

f''(x)  =  -1/(1-x)²

f''(0)  =  -1

f'''(x)  =  -2/(1-x)³

f'''(0)  =  -2

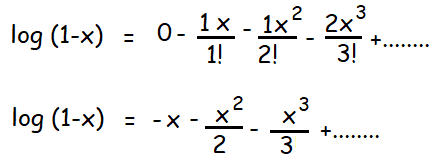
(v)  tan^-1 x ; -1 ≤ x ≤ 1

Solution :

f(x)  =  tan^-1 x

f(0)  =  tan^-1 (0)  ==>  0

f'(x)  =  1/(1+x²)

f'(x)  =  (1+x²)^-1

f'(x)  =  1 - x² + x⁴ - x⁶ +...............

f'(0)  =  1

f''(x)  =  0 - 2x + 4x³ - 6x⁵ +...............

f''(0)  =  0

f'''(x)  =  -2 + 12x² - 30x⁴ +...............

f'''(0)  =  -2

f'^v(x)  =  24x - 120x³ +...............

f'^v(0)  =  0

f^v(x)  =  24 - 360x² +...............

f^v(0)  =  24

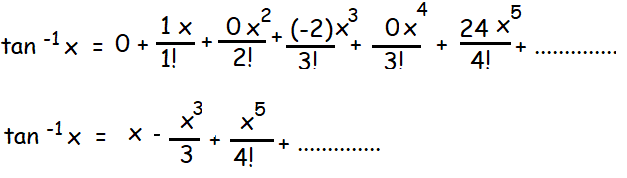
(vi)  cos² x

Solution :

f(x)  =  cos² x

f(0)  =  cos² (0) 

f(0)  =  1

f'(x)  =  2cos x (-sin x)

f'(x)  =  -sin 2x

f'(0)  =  -sin 2(0)  =  0

f''(x)  =  -cos 2x (2)

f''(x)  =  -2cos 2x

f''(0)  =  -2cos 2(0)  ==>  -2

f'''(x)  =  4sin 2x

f'''(0)  =  4sin 2(0)  ==>  0

f'^v(x)  =  8cos 2x

f'^v(0)  =  8cos 2(0)  ==>  8

cos²x  =  1 + (0x)/1! + (-2)x²/2! + 0x³/3! + 8x⁴/4! +.......

cos²x  =  1 - x² + x⁴/3 +.......

Problem 2 :

Write down the Taylor series expansion, of the function log x about x = 1 upto three non-zero terms for x > 0

Solution :

f(x)  =  log x

f(x)  =  f(1) + [(x-1)/1!] f'(1) + [(x-1)²/2!] f''(1)

+ [(x-1)³/3!] f'''(1) +................

f(x)  =  log x

f(1)  =  log 1  ==>  0

f'(x)  =  1/x

f'(1)  =  1/1  ==>  1

f''(x)  =  -1/x²

f''(1)  =  -1/1²  ==>  -1

f'''(x)  =  1/x³

f'''(1)  =  1/1³  ==>  1

log x  =  0 + [(x-1)/1!](1) + [(x-1)²/2!] (-1)

+ [(x-1)³/3!] (1) +................

log x  =  (x-1) - [(x-1)²/2] + [(x-1)³/6] (1) +................

Problem 3 :

Expand sin x in ascending powers x-π/4 upto three non zero terms.

Solution :

f(x)  =  sin x

x  =  x-π/4

f(π/4)  =  sin π/4  =  1/√2

f'(x)  =  cos x : f'(π/4)  =  1/√2

f''(x)  =  -sin x : f''(π/4)  =  -1/√2

f(x)  =  f(π/4) + [(x-π/4)/1!] f'(π/4) + [(x-π/4)²/2!] f''(π/4) + [(x-π/4)³/3!] f'''(π/4) +................

f(x)  =  (1/√2) + (x-π/4) (1/√2) + [(x-π/4)²/2] (-1/√2)

 + [(x-π/4)³/6] (-1/√2) +................

f(x)  =  (1/√2)[1 + (x-π/4) - [(x-π/4)²/2]

 - [(x-π/4)³/6] +................

Problem 4 :

Expand the polynomial f(x)  =  x²-3x+2 in powers of x-1.

Solution :

f(x)  =  x²-3x+2

f(1)  =  1²-3(1)+2  =  0

f'(x)  =  2x-3

f'(1)  =  2(1)-3  =  -1

f''(x)  =  2

f(x)  =  f(1)+[(x-1)/1!]f'(1)+[(x-1)²/2!]f''(1)

 +[(x-1)³/3!]f'''(1)................

f(x)  =  0+[(x-1)/1!](-1)+[(x-1)²/2!](2)

f(x)  =  -(x-1)+(x-1)²

Problem 5 :

a)  Find the Maclaurin series for the function f(x) = ln(1 + x) and hence that for ln (1 + x)/x

b) By keeping the first four terms in the Maclaurin series for ln(1 + x)/x integrate the function ln (1 + x)/x from x = 0 and x = 1.

c) Estimate the magnitude and sign of the error made is evaluating the integral in this way.

d) Confirm that your results are consistent with alternating series estimation theorem by evaluating the integral on the GCD.

Solution :

a) 

f(x) = ln (1 + x)

Let x = 0

f(0) = ln (1 + 0)/0

= 0  -----(1)

f'(x) = 1/(1 + x)

f'(0) = 1/(1 + 0)

f'(0) = 1  -----(2)

f'(x) = (1 + x)^-1

f''(x) = -1(1 + x)^-2

f''(0) = -1(1 + 0)^-2

= -1  -----(3)

f'''(x) = -1(-2) (1 + x)^-3

= 2 (1 + x)^-3

f'''(0) = 2 (1 + 0)^-3

= 2(1/1)³

= 2  -----(4)

f'^v(x) = 2(-3) (1 + x)^-4

= -6 (1 + x)^-4

f^iv(0) = -6 (1 + x)^-4

= -6(1  + 0)^-4

= -6  -----(5)

f(x) = f(0) + [f'(0)/1!]x + [f''(0)/2!] x² + [f'''(0)/3!] x³ + ..........

ln (1 + x) = 0 + (1/1!)x + (-1/2!) x² + (2/3!) x³ + (-6/4!) x⁴ + ...........

= x - (x²/2) + (2x³/6) + (-6x⁴/24)  + ...........

ln (1 + x) = x - (x²/2) + (x³/3) - (x⁴/4)  + ...........

ln (1 + x)/x = (x - (x²/2) + (x³/3) - (x⁴/4)  + ...........)/x

= 1 - x/2 + (x²/3) - (x³/4)  + ...........

b) Integrate the above expansion, we get

= x - x²/4 + x³/9 - x⁴/16 + ............

Applying the limits, we get

= 1 - 1²/4 + 1³/9 - 1⁴/16 + ............

= 1 - 0.25 + 0.1111...- 0.0625 +......

= 0.7985.......

(c) The error is less in magnitude than the first term neglected i.e. 1/5² =0.0400 and has the same sign (i.e. positive) so the estimate is an underestimate.

(d)The value of the integral is 0.8225. The error is thus 0.8225 - 0.7986 = +0.0239.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.