FIND LOCAL MAXIMUM AND LOCAL MINIMUM OF A FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If f(x) is differentiable on the interval, except possibly at c, then f (c) can be classified as follows:
(when moving across the interval I from left to right)
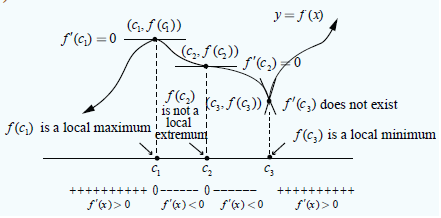
(i) If f′(x) changes from negative to positive at c , then f (x) has a local minimum f (c) .
(ii) If f′(x) changes from positive to negative at c , then f (x) has a local maximum f (c) .
(iii) If f′(x) is positive on both sides of c or negative on both sides of c , then f (c) is neither a local minimum nor a local maximum.
Find the intervals of monotonicities and hence find the local extremum for the following functions:
Problem 1 :
f(x) = 2x3 + 3x2 −12x
Solution :
f(x) = 2x3 + 3x2 −12x
f'(x) = 6x2+6x-12
f'(x) = 0
6x2+6x-12 = 0
6(x2+x-2) = 0
(x+2)(x-1) = 0
x = -2 and x = 1
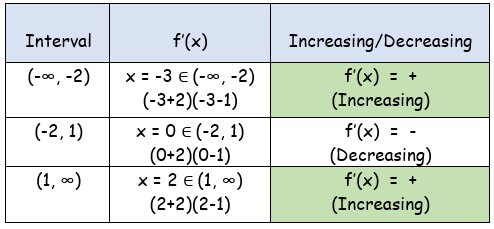
f'(x) changes from positive to negative when it passes through x = -2, so it has local maximum at x = -2.
Local maximum at x = -2 :
f(-2) = 2(-2)3 + 3(-2)2 −12(-2)
f(-2) = 2(-8) + 3(4) + 24
f(-2) = -16 + 12 + 24
f(-2) = 20
f'(x) changes from negative to positive when it passes through x = -2, so it has local maximum at x = 1.
Local minimum at x = 1 :
f(1) = 2(1)3 + 3(1)2 −12(1)
f(1) = 2+3-12
f(1) = -7
So, local maximum is 20 and local minimum is -7.
Problem 2 :
f(x) = x/(x-5)
Solution :
f(x) = x/(x-5)
u = x and v = x-5
u' = 1 and v' = 1
f'(x) = [(x-5)(1) - x(1)]/(x-5)2
f'(x) = -5 < 0
It is strictly decreasing, so there is no local extrema.
Problem 3 :
f(x) = ex/(1-ex)
Solution :
f(x) = ex/(1-ex)
u = ex and v = 1-ex
u' = ex and v' = -ex
f'(x) = [(1-ex)ex - ex(-ex)]/(1-ex)2
f'(x) = ex/(1-ex)2 > 0
It is strictly increasing, so there is no local extrema.
Problem 4 :
f(x) = (x3/3) - log x
Solution :
f(x) = (x3/3) - log x
f'(x) = (3x2/3) - (1/x)
f'(x) = x2 - (1/x)
f'(x) = (x3 - 1)/x
f'(x) = (x3 - 1)/x
x3 - 1 = 0
x3 = 1
x = 1
The domain of the given function is (0, ∞).
So, the intervals are (0, 1) and (1, ∞).

The function is strictly decreasing at (0, 1). f'(x) changes its sign from negative to positive, so it will have local minimum at x = 1.
Local minimum at x = 1 :
f(1) = (13/3) - log 1
f(1) = 1/3
Problem 5 :
f(x) = sinx cosx + 5, x ∈ (0, 2π)
Solution :
f(x) = (2/2)sinx cosx + 5
f(x) = (1/2) sin 2x + 5
f'(x) = (2/2) cos 2x
f'(x) = cos 2x
f'(x) = 0
cos 2x = 0
2x = cos-1(0)
2x = π/2, 3π/2, 5π/2, 7π/2
x = π/4, 3π/4, 5π/4, 7π/4
So, the intervals are
(0, π/4), (π/4, 3π/4), (3π/4, 5π/4), (5π/4, 7π/4)
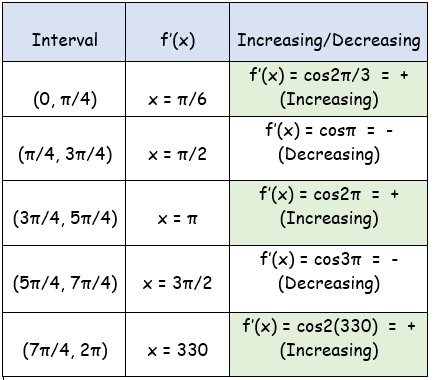
- At x = π/4, f'(x) changes from positive to negative. So, local maximum at x = π/4.
- At x = 3π/4, f'(x) changes from negative to positive. So, local minimum at x = 3π/4.
- At x = 5π/4, f'(x) changes from positive to negative. So, local maximum at x = 5π/4.
- At x = 7π/4, f'(x) changes from negative to positive. So, local minimum at x = 7π/4.
Local Minimum at x = π/4 :
f(π/4) = (1/2) sin 2(π/4) + 5 ==> 11/2
Local Maximum at x = 3π/4 :
f(3π/4) = (1/2) sin 2(3π/4) + 5
= (1/2) (-1) + 5
= (-1/2)+5
= 9/2
Problem 6 :
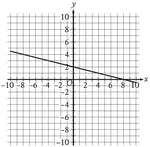
Let f be a function defined on the closed interval −5 ≤ x ≤ 5 with f(1) = 3 . The graph of f', the derivative of f, consists of two semicircles and two line segments, as shown above.
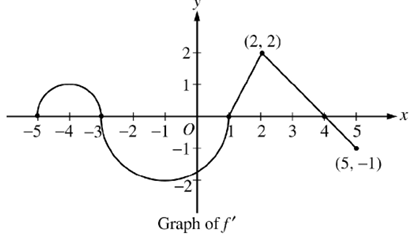
(a) For −5 < x < 5 , find all values of x at which f has a relative maximum. Justify your answer.
(b) For −5 < x < 5 , find all values of x at which f has a point of inflection. Justify your answer.
(c) Find all intervals on which the graph of f (not shown) is concave up. Justify your answer.
(d) Find all intervals on which the graph of f (not shown) has a positive slope. Justify your answer.
Solution :
a)
- In the interval [-3, 1] the graph of the first derivative is below the x-axis. Then it is decreasing in this interval.
- In the interval [-5, -3] and [1, 4], the graph is above the x-axis. Then it is increasing in this interval.
- In the interval [4, 5], the graph is below the x-axis. Then it is decreasing in this interval.
So, f has a relative maximum at x =−3 and x = 4 because f'(x) changes signs from positive to negative.
b) f has a point of inflection at 4, -1, and 2 because f" changes signs
c) f is concave up on (-5, -4) and (-1, 2) because f' is increasing or f " > 0.
d) f has a positive slope on (-5, -3) and (1, 4) because f'(x) > 0.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 23)
Feb 27, 26 04:01 AM
Digital SAT Math Problems and Solutions (Part - 23) -
Digital SAT Math Problems and Solutions (Part - 22)
Feb 26, 26 08:43 PM
Digital SAT Math Problems and Solutions (Part - 22) -
10 Tricky SAT Math Questions with Answers
Feb 25, 26 08:07 AM
10 Tricky SAT Math Questions with Answers