RATIONAL EXPONENTS 

We use radical symbol √ to indicate roots. The index is the small number to the left of the radical symbol that says which root has to be taken.

For example, ³√ represents a cube root. Because, 

2³  =  2 ⋅ 2 ⋅ 2  =  8,  ³√8  =  2

Another way to write n^th roots is by using exponents that are fractions.  

For example, for a > 1, suppose √a  =  a^m, then

√a  =  a^m

Square both sides. 

(√a)²  =  (a^m)²

Power of a Power Property.

a¹  =  a^2m

If two terms are equal with the same base, then the exponents must be equal. 

1  =  2m

Divide each side by 2.

1/2  =  m

So, for all a > 1, √a  =  a^1/2.

Definition of a^1/n :

Words :

A number raised to the power of 1/n is equal to the n^th root of that number. 

Numbers :

5^1/2  =  √5

3^1/4  =  ⁴√3

4^1/7  =  ⁷√4

Algebra :

If a > 1 and n is an integer, where n ≥ 2, then 

a^1/n  =  ⁿ√a

And also, 

a^1/2  =  √a

a^1/3  =  ³√a

a^1/4  =  ⁴√a

and so on. 

Example 1 : 

Simplify :

64^1/3

Solution : 

=  64^1/3

Use the definition of a^1/n.

=  ³√64

=  ³√(4³)

=  4

Example 2 : 

Simplify :

81^1/4

Solution : 

=  81^1/4

Use the definition of a^1/n.

=  ⁴√81

=  ⁴√(3⁴)

=  3

Example 3 : 

Simplify :

32^1/5 + 100^1/2

Solution : 

=  32^1/5 + 100^1/2

Use the definition of a^1/n.

=  ⁵√32 + √100

=  ⁵√(2⁵) + √(10²)

=  2 + 10

=  12

Example 4 : 

Simplify :

121^1/2 + 256^1/4

Solution : 

=  121^1/2 + 256^1/4

Use the definition of a^1/n.

=  √121 + ⁴√256

=  √(11²) + ⁴√(4⁴)

=  11 + 4

=  15

Numerator Other than 1 

A fractional exponent can have a numerator other than 1, as in the expression b^2/3. 

You can write the exponent as a product in two different ways as shown below.  

Definition of a^m/n :

Words :

A number raised to the power of m/n is equal to the n^th root of the number raised to m^th power.

Numbers :

8^2/3  =  (³√8)²  =  2²  =  4

or

8^2/3  =  ³√(8²)  =  ³√64  =  4

Algebra :

If a > 1 and m and n are integers, where n ≥ 1 and n ≥ 2, then 

a^m/n  =  (ⁿ√a)^m  =  ⁿ√(a^m)

Example 5 : 

Simplify :

216^2/3

Solution : 

=  216^2/3

Use the definition of a^m/n.

=  (³√216)²

=  (³√6³)²

=  (6)²

=  36

Example 6 : 

Simplify :

32^4/5

Solution : 

=  32^4/5

Use the definition of a^m/n.

=  (⁵√32)⁴

=  (⁵√2⁵)⁴

=  (2)⁴

=  16

Example 7 : 

Simplify :

27^4/3

Solution : 

=  27^4/3

Use the definition of a^m/n.

=  (³√27)⁴

=  (³√3³)⁴

=  (3)⁴

=  81

Note :

Remember that √ always indicate a nonnegative square root. When you simplify variable expressions that contain √, such as √x², the answer can not be negative. But x may be negative. Therefore you simplify √x² as |x| to ensure the answer is nonnegative. 

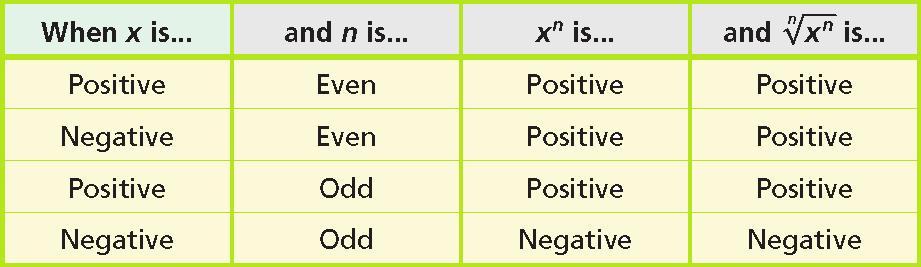
When n is even, you must simplify ⁿ√xⁿ, to |x|, because you do not know whether x is positive or negative. When n is odd, simplify ⁿ√xⁿ, to x. 

ⁿ√xⁿ  =  |x|, when n is even

ⁿ√xⁿ  =  x, when n is odd

Example 8 : 

Simplify :

³√(x⁹y³)

Solution : 

=  ³√(x⁹y³)

Use the definition of a^m/n.

=  (x⁹y³)^1/3

Power of a Product Property.

=  (x⁹)^1/3 ⋅ (y³)^1/3

Power of a Power Property.

=  (x^9 ⋅ 1/3) ⋅ (y^3 ⋅ 1/3)

Simplify exponents. 

=  (x³) ⋅ (y¹)

=  x³y

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.