EXPLORING GRAPHS OF RATIONAL FUNCTIONS

Understanding the graphs of rational functions is sometimes a difficult stuff for some student who study math in both school level and college level. 

Actually, it is not a difficult one. We can understand the graphs of rational functions when we explore them in a proper way. 

To explore the graphs of rational functions, let us consider the example which is given below. 

Rational Function - Example

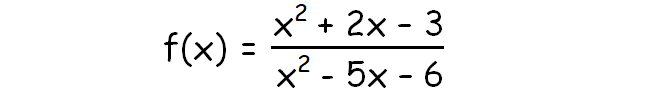
In the process of exploring graphs of rational functions, first we have to know the following stuff. 

1. Vertical Asymptote

2. Horizontal Asymptote

3. Slant Asymptote

4. Hole

To know more about the above mentioned stuff, please click the topics given above.

If you had already learned the above mentioned stuff, then you are ready to learn the stuff, "How to graph rational functions".

Now let us take an example and explore the graphs of rational functions.

Example :

Graph the rational function given below.

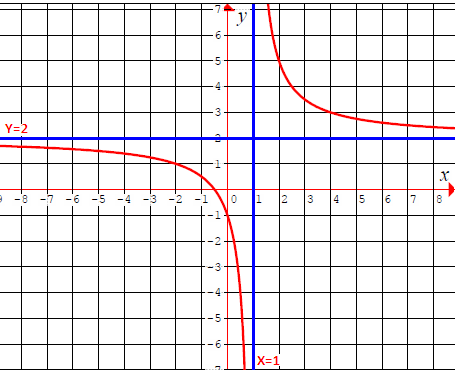
y  =  (2x + 1) / (x - 1)

Solution :

Step 1 :

First, we have to find hole, if any.

To find hole of the rational function, we have to see whether there is any common factor found at both numerator and denominator.

In our problem, clearly there is no common factor found at both numerator and  denominator.So, there is no hole.

Step 2 :

Now, we have to find vertical asymptote, if any. 

Most of the rational function will have vertical asymptote. 

To find vertical asymptote, we have to make the denominator equal to zero.

When we do so,    x - 1 = 0  ====>    x  =  1

So, the vertical asymptote is   x  =  1

Step 3 :

Now we have to find horizontal asymptote, if any.

In the rational function given above, the highest exponent of the numerator and denominator are equal. So there is an horizontal asymptote. 

Equation of the horizontal asymptote:

y = a/b

Here 'a' and 'b' are the coefficients of highest exponent terms at the numerator and denominator respectively.  

In our problem,   a  =  2  and b  =  1

So, horizontal asymptote is

y  =  2/1

y  =  2

Step 4 :

Now we have to find slant asymptote, if any.

Since there is horizontal asymptote, there is no slant asymptote.

Step 5 :

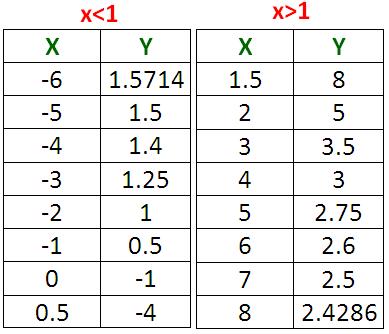
In the given rational function, now we have to plug some random values for x and find the corresponding values of y. 

We have already known that the vertical asymptote is

x  =  1 

Now, we have to take some random values for x on the left side of x = 1 as well as right side of x = 1 (as given in the table below).

That is, 

x < 1 and x > 1 but x ≠ 1

(Because, x = 1 is vertical asymptote)

Apart from the stuff given above, if you need any other stuff, please use our google custom search here.   

If you have any feedback about our math content, please mail us : 

v4formath@gmail.com

We always appreciate your feedback. 

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6