EXPECTED VALUE OF A DISCRETE RANDOM VARIABLE

Expected value or Mathematical Expectation or Expectation of a random variable may be defined as the sum of products of the different values taken by the random variable and the corresponding probabilities.

For example, if a discrete random variable takes the values 1, 2, 3, 4 and 5, expected value of the random variable is nothing but the most probable value among the values 1, 2, 3, 4 and 5.   

That is, the value which has more chance to occur.

Let "X" be a discrete random variable.

Let us assume that  X takes n values X1, X2, X3........Xn with corresponding probabilities P1, P2, P3 …., Pn 

Then, the expected value is given by 

E(X)  =  ∑PiXi

Expected value of x² is given by

E(X²)  =  ∑PiXi²

When x is a discrete random variable with probability mass function f(x), then its expected value is given by

E(x)  =  ∑xf(x)

Note :

Expected value is also called as mean

Properties of Expected Value

1.  Expectation of a constant k is k

That is,

E(k) = k for any constant k

2.  Expectation of sum of two random variables is the sum of their expectations.

That is,

E(x + y) = E(x) + E(y) for any two random variables x and y.

3.  Expectation of the product of a constant and a random variable is the product of the constant and the expectation of the random variable.

That is, 

E(kx) = k.E(x) for any constant k

4. Expectation of the product of two random variables is the product of the expectation of the two random variables, provided the two variables are independent.

That is,

E(xy) = E(x).E(y)

Whenever x and y are independent.

Examples

Example 1 :

An unbiased coin is tossed three times. Find the expected value of the number of heads.

Solution :

Let x denote the number of heads when an unbiased coin is tossed three times.

Then the possible values of x are 0, 1, 2 and 3.

The probability distribution of x is given by

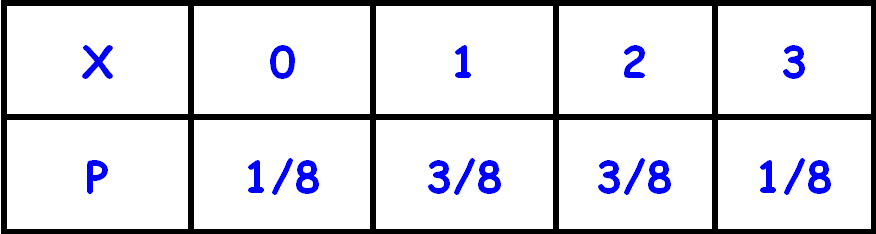
Now, the expected value of x is given by

E(x)  =  ∑px

E(x)  =  (0x1/8) + (1x3/8) + (2x3/8) + (3x1/8)

E(x)  =  0 + 3/8 + 6/8 + 3/8

E(x)  =  (3 + 6 + 3) / 8

E(x)  =  12/8

E(x)  =  1.5

So, the expected value of number of heads is 1.5

Example 2 :

In a business venture, a man can make a profit of $ 50000 or incur a loss of $20000. The probabilities of making profit or incurring loss, from the past experience, are known to be 0.75 and 0.25 respectively. What is his expected profit ?

Solution :

Let x denote the profit in business.  

Then the possible values of x are 50000 and -20000.

(20000 loss can be taken as -20000 profit)

The probability distribution of x is given by

Now, the expected value of "x" is given by

E(x)  =  ∑px

E(x)  =  (50000x0.75) + (-20000x0.25)

E(x)  =  37500 - 5000

E(x)  =  32500

So, the expected profit is $32500.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.