EQUATION OF THE TANGENT TO ELLIPSE FROM THE POINT WITHOUT DERIVATION

Example 1 :

Find the equation of tangent to the ellipse

4x²+9y²  =  36

at (2, 2).

Solution :

Equation of tangent to ellipse will be in the form

y  =  mx+√(a²m²+b²)

From equation of ellipse, we may derive the values of a² and b²

Equation of ellipse :

4x²+9y²  =  36

Divide by 36, we get

(x²/9) + (y²/4)  =  1

a²  =  9, b²  =  4

Equation of tangent :

y  =  mx+√(9m²+4)  ----(1)

Equation of tangent at (2, 2) :

2  =  m(2)+√(9m²+4)

2  =  2m+√(9m²+4)

(2-2m)  =  √(9m²+4)

Taking squares on both sides, we get

(2-2m)²  =  (9m²+4)

4-8m+4m²  =  9m²+4

5m²+8m  =  0

m(5m + 8)  =  0

m  =  0 and m  =  -8/5

By applying the values of m in (1), we get

y  =  mx+√(9m²+4)  ----(1)

So, the required equations of tangent are

y-2 = 0 and 8x-5y-26 = 0

Example 2 :

Find the equations of the two tangents that can be drawn from the point (5, 2) to the ellipse

2x² + 7y² = 14

Solution :

Equation of ellipse :

2x² + 7y²  =  14

Dividing by 14

x²/7 + y²/2  =  1

a²  =  7, b²  =  2

Equation of tangent :

y  =  mx+√(7m²+2)  ----(1)

Equation of tangent at (5, 2) :

2  =  m(5)+√(7m²+2)

2  =  5m+√(7m²+2)

(2-5m)  =  √(7m²+2)

Taking squares on both sides, we get

(2-5m)²  =  (7m²+2)

4-20m+25m²  =  7m²+2

18m²-20m+2  =  0

9m²-10m+1  =  0

m  =  1 and m  =  1/9

By applying the values of m in (1), we get

y  =  mx+√(7m²+2)  ----(1)

So, the required equations of tangent are

x-y-3 = 0 and x+9y-13 = 0

Example 3 :

Tangents are drawn from a point (3, 4) to the ellipse

(x²/9) + (y²/4) = 1

touching ellipse at the point A and B. The equation of the locus of the point whose distances from the point P and the line AB are equal is.

Solution :

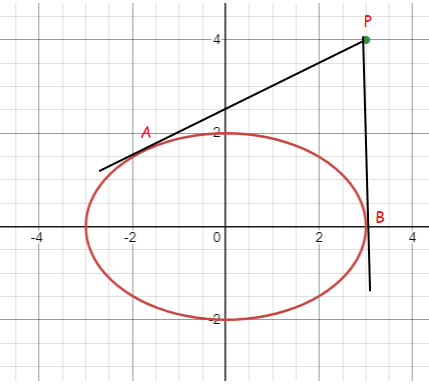
AB is the chord of the ellipse, let (h, k) be any point on the locus.

Distance between the point (3, 4) and (h, k) is equal to the distance from the point (3, 4) and chord of the ellipse at the point (h, k).

Equation of tangent :

Change x² as xx₁ and y² as yy₁

(xx₁/9) + ( yy₁/4) = 1

Applying the point (3, 4), we get

(3x/9) + (4y/4) = 1

(12x + 36y)/36 = 1

12x + 36y = 36

Dividing by 12, we get

x + 3y = 3

Distance between the points (3, 4) and (h, k)

√(h - 3)² + (k - 4)²

Distance between (h, k) and chord of ellipse

= |h + 3k - 3| / √(1² + 3²)

= |h + 3k - 3| / √10

√(h - 3)² + (k - 4)² = |h + 3k - 3| / √10

Squaring on both sides 

(h - 3)² + (k - 4)² = (h + 3k - 3)²/ 10

10(h² - 6h + 9 + k² - 8k + 16) = h² + 9k² + 9 + 6hk - 18k - 6h

10h² - 60h + 90 + 10k² - 80k + 160 = h² + 9k² + 9 + 6hk - 18k - 6h

10h² - h²- 60h + 6h + 90 + 10k² - 9k² - 80k + 18k + 160 - 9  - 6hk = 0

9h² + k² - 54h - 62k - 6hk + 232 = 0

Changing (x, y), we get

9x² + y² - 54x - 62y - 6xy + 232 = 0

Example 4 :

Find the equations of the tangents drawn from the point (2, 3) to the ellipse 9x² + 16y² =  144

Solution :

Equation of ellipse :

9x² + 16y² =  144

Dividing by 144

x²/16 + y²/9  =  1

a² = 16, b² = 9

Equation of tangent :

y  =  mx + √(16m² + 9)  ----(1)

Equation of tangent at (2, 3) :

3 = m(2) + √(16m² + 9)

3 = 2m + √(16m² + 9)

(3 - 2m)  =  √(16m² + 9)

Taking squares on both sides, we get

(3 - 2m)²  =  (16m² + 9)

9 - 12m + 4m² = 16m² + 9

16m² - 4m² + 12m + 9 - 9 = 0

12m² + 12m = 0

12m(m + 1) = 0

m = 0 and m = -1

So, the required equations of tangents from the given points are y = 3 and y = -x + 5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.