EASY WAY TO EXPAND BINOMIALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Pascal triangle is one of the good applications in mathematics that can be used to expand binomial expressions with any power.
Let us see how pascal triangle can be used to expand
(a + b)n
for any value of n.
Pascal Triangle and Exponent of the Binomial

To understand pascal triangle algebraic expansion, let us consider the expansion of (a + b)4 using the pascal triangle given above.
How to Get Expansion of (a + b)⁴ Using Pascal Triangle
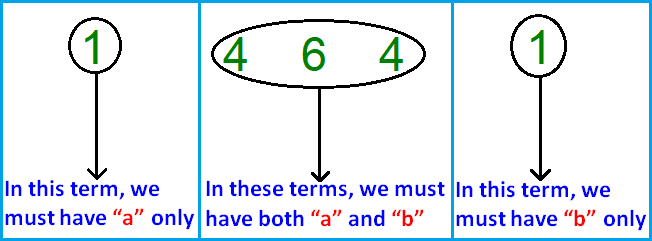
In (a + b)4, the exponent is '4'.
So, let us take the row in the above pascal triangle which is corresponding to 4th power.
That is,
1 4 6 4 1
General Rule :
In pascal expansion, we must have only 'a' in the first term, only 'b' in the last term and 'ab' in all other middle terms.
If we are trying to get expansion of (a + b)n, all the terms in the expansion will be positive.
Note :
This rule is not only applicable for power '4'.
This rule is applicable for any value of 'n' in (a + b)ⁿ.
It has been clearly explained below.
Now we have to follow the steps given below.
Step 1 :
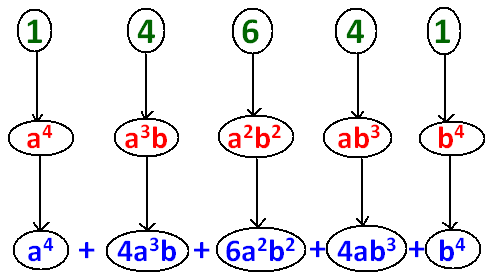
In the first term, we have to take only 'a' with power '4' [This is the exponent of (a + b)].
Then, the first term will be a4.
Step 2 :
In the second term, we have to take both 'a' and 'b'.
For 'a', we have to take exponent '1' less than the exponent of 'a' in the previous term.
For 'b', we have to take exponent '1'.
Then, the second term will be a3b.
Step 3 :
In the third term also, we have to take both 'a' and 'b'.
For 'a', we have to take exponent '1' less than the exponent of 'a' in the previous term.
For 'b', we have to take exponent '2'.
Then, the second term will be a2b2.
(We have to continue this process, until we get the exponent '0' for 'a')
Step 4 :
When we continue the process said in step 3, the term in which we get exponent '0' for 'a' will be the last term.
In the last term, we will have only 'b' with power '4' [This is the exponent of (a + b)].
Then, the last term will be b4.
The four steps explained above given in the picture below.
Finally the expansion is,
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
How to Get Expansion of (a - b)⁴ Using Pascal Triangle
General Rule :
If we are trying to get expansion of (a - b)n, we have to take positive and negative signs alternatively staring with positive sign for the first term.
Note :
This rule is not only applicable for power '4', this rule is applicable for any value of 'n' in (a - b)n.
To get expansion of (a - b)4, we do not have to do much work.
As we have explained above, we can get the expansion of (a + b)4 and then we have to take positive and negative signs alternatively staring with positive sign for the first term
So, the expansion is
(a - b)4 = a4 - 4a3b + 6a2b2 - 4ab3 + b4
In this way, using pascal triangle to get expansion of a binomial with any exponent.
Expand the following binomials using pascal triangle :
Example 1 :
(3x + 4y)4
Solution :
Already, we know
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Comparing (3x + 4y)4 and (a + b)4, we get
a = 3x and b = 4y
Substitute a = 3x, b = 4y in the expansion of (a + b)4.
So, we have
(3x + 4y)4 = (3x)4 + 4(3x)3(4y) + 6(3x)2(4y)2 + 4(3x)(4y)3 + (4y)4
(3x + 4y)4 = 81x4 + 4(27x3)(4y) + 6(9x2)(16y2) + 4(3x)(64y3) + 256y4
(3x + 4y)4 = 81x4 + 432x3y + 864x2y2 + 768xy3 + 256y4
Example 2 :
Expand the following using pascal triangle
(p - 4q)4
Solution :
Already, we know
(a - b)4 = a4 - 4a3b + 6a2b2 - 4ab3 + b4
Comparing (p - 4q)4 and (a - b)4, we get
a = p and b = 4q
Substitute a = p and b = 4q in the expansion of (a - b)4.
(p - 4q)4 = p4 - 4(p3)(4q) + 6(p2)(4q)2 - 4(p)(4q)3 + (4q)4
(p - 4q)4 = p4 - 16p3q + 6(p2)(16q2) - 4(p)(64q3) + 256q4
(p - 4q)4 = p4 - 16p3q + 96p2q2 - 256pq3 + 256q4
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos
