DOMAIN AND RANGE OF FUNCTIONS

How to find the domain and range of a relation given by a set of ordered pairs ?

Domain is nothing but the values of "x" for which the given function is defined. 

Range is nothing but the values of "y" that we get for the the given domain (values of "x"). 

Example 1 :

Which of the following relations are functions from

A = { 1, 4, 9, 16 } to B = { –1, 2, –3, –4, 5, 6 }

In case of a function, write down its domain and range.

f₁ = { (1, –1), (4, 2), (9, –3), (16, –4) }

Solution :

From the set of ordered pairs, the list of first elements are domain and second elements are range.

Domain  =  {1, 4, 9, 16}

Range  =  {-1, 2, -3, -4}

Co domain  =  { –1, 2, –3, –4, 5, 6 }

To see more examples, please click on the link.

How to find the domain and range from a relation

How to find domain and range of a mapping diagram ?

Example 2 : 

Let A  =  {1, 2, 3} and B  =  {5, 6, 7, 8}. 

f is the function which maps the elements from A to B as shown below. 

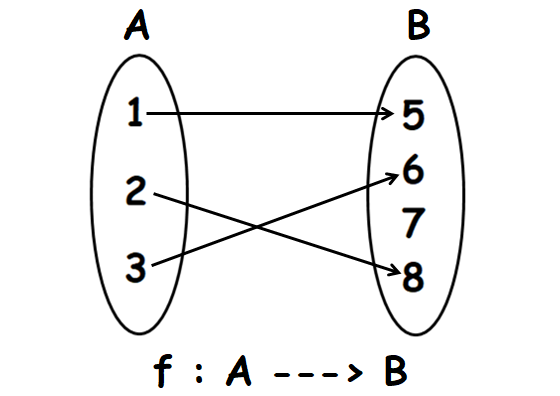
Find, the domain, co-domain and range of f. 

Solution :

Domain (f)  =  A  =  {1, 2, 3}

Co-domain (f)  =  B  =  {5, 6, 7, 8}

Range (f)  =  {5, 6, 7} 

To get more example,

Domain codomain and range of a function

How to find domain and range of a mapping diagram

Domain and Range from Graph

Domain :

The domain is the set of possible input values, which are shown horizontally on the x-axis.

Range :

The range is the set of possible output values, which are shown vertically on the y-axis.

Example 3 :

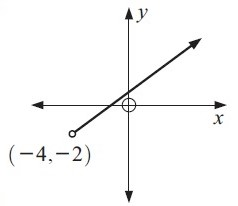
Solution :

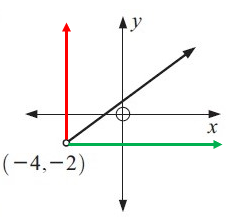
Finding the domain :

In the given graph, the possible values of x are -4, -3, -2 ……… there are spread horizontally on the x-axis.

Because the graph starts at -4 on the x-axis.

So, the domain (x) is x > -4

Finding the range :

In the given graph, the possible values of y are -2, -1, 0 ……… there are spread vertically on the y-axis.

Because the graph starts at -2 on the y-axis.

So, the range (y) is y > -2

To see more examples,

find domain and range from a graph

Domain and Range of Polynomial Function

Example 4 :

Find the domain of the following function

f(x)  =  1 / (x + 2)

Solution :

The given function accepts all real values except -2. In the given function if we apply -2 instead of x, it will become undefined.

Hence the domain of f(x) is R - {-2}

Example 5 :

Joe had a summer job that pays $7.00 an hour and he worked between 15 and 35 hours every week. His weekly salary can be modeled by the equation:

S = 7h

where S is his weekly salary and h is the number of hours he worked in a week.

a. Describe the independent variable for this problem.

b. Describe the domain and range for this problem using appropriate notation.

Domain:

Range:

c. What does each value in the ordered pair (20, 140) mean in context of this problem?

Solution :

S = 7h

a. In the given function number of hours he worked is the independent variable and his weekly salary is dependent variable.

b. Minimum number of hours working is 15 and maximum number of hours working is 35.

Then domain is 15 ≤ h ≤ 35

• When h = 15, S = 7(15) ==> 105
• When h = 35, S = 7(35) ==> 245

Range is 105 ≤ S ≤ 245

c. 20 = number of hours worked and 140 = his weekly salary.

Example 6 :

Hector’s service club is raising money by wrapping presents in the mall. The function

f(x) = 3x

describes the amount of money, in dollars, the club will earn for wrapping x presents. They only have enough wrapping paper to wrap 1000 presents.

a. Describe the dependent variable for this problem.

b. Describe the domain and range for this problem using appropriate notation. Domain: Range:

Solution :

a. number of presents is independent variable and amount of money for wrapping it is the dependent variable.

b. Minimum number of presents = 0 and maximum number of presents = 1000

Domain is 0 ≤ x ≤ 1000

• When x = 0, f(0) = 3(0) ==> 0
• When x = 1000, f(1000) = 3(1000) ==> 3000

Range is 0 ≤ f(x) ≤ 3000

To see more examples.

Domain of a function worksheet

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.