HOW TO FIND THE DOMAIN AND RANGE FROM A RELATION

Let f₁, f₂, f₃ , f₄ and f₅ be the relations defined from A to B. If A = {1, 4, 9, 16} and B = {–1, 2, –3, –4, 5, 6}, Which of the following relations are functions ? In case of a function, write down its domain and range.

Example 1 :

f₁ = {(1, –1), (4, 2), (9, –3), (16, –4)}

Solution :

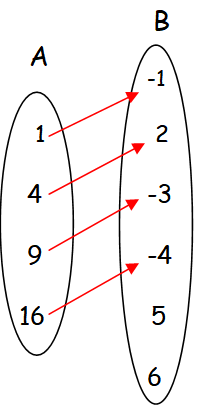
In the above arrow diagram, each element of A has image in B and also each element of A has only one image in A.

So the relation f₁ is a function.

Domain is the elements of A. 

Domain = {1, 4, 9, 16}

Range is the elements of B which have preimages in A.

Range = {-1, 2, -3, -4}

Example 2 :

f₂ = {(1, –4), (1, –1), (9, –3), (16, 2)}

Solution :

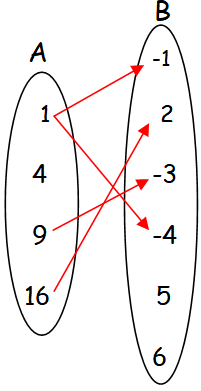
In the above arrow diagram, element 4 in A does not have image in B.

So the relation f₂ is not a function.

Example 3 : 

f₃ = {(4, 2), (1, 2), (9, 2), (16, 2)}

Solution :

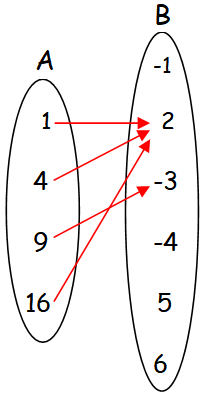
In the above arrow diagram, each element of A has image in B and also each element of A has only one image in A.

So the relation f₃ is a function.

Domain is the elements of A. 

Domain = {1, 4, 9, 16}

Range is the elements of B which have preimages in A.

Range = {2, -3}

Example 4 :

f₄ = {(1, 2), (4, 5), (9, –4), (16, 5)}

Solution :

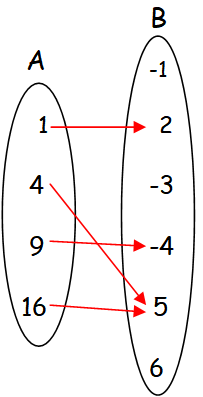
In the above arrow diagram, each element of A has image in B and also each element of A has only one image in A.

So the relation f₄ is a function.

Domain is the elements of A. 

Domain = {1, 4, 9, 16}

Range is the elements of B which have preimages in A.

Range = {2, -4, 5}

Example 5 :

f₅ = {(1, 2), (4, -3), (4, 5), (9, –4), (16, 5)}

Solution :

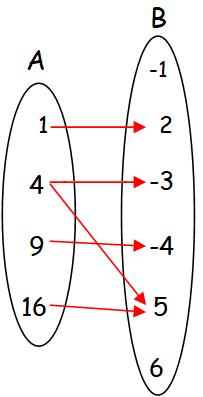
In the above arrow diagram, each element of A has image in B. But the element 4 in A has more than one image in B (two images -> -3 and 5).

So the relation f₅ is not a function.

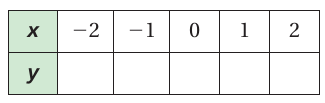
• Copy and complete each input-output table.
• Find the domain and range of the function represented by the table.

Example 6 :

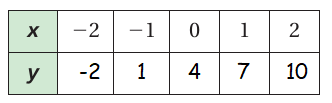
y = 3x + 4

Solution :

When x = 2

y = 3(2) + 4

= 6 + 4

= 10

Example 7 :

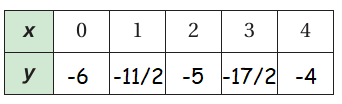
y = (1/2)x - 6

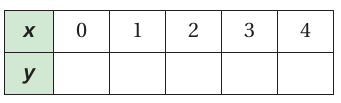
Solution :

When x = 4

y = (1/2)(4) - 6

= 2 - 6

= -4

Example 8 :

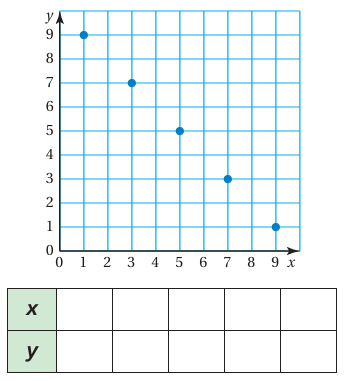
Solution :

Set of ordered pairs from the points plotted,

(1, 9) (3, 7) (5, 5) (7, 3) (9, 1)

The values of x are :

1, 3, 5, 7, 9

The values of y are :

9, 7, 5, 3, 1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.