DETERMINING THE NUMBER OF SOLUTIONS

When we solve a linear equation in one variable, we may find exactly one value of x that will make the equation a true statement. But, when we simplify some equations, we may find that they have more than one solution or they do not have solution.

The table given below explains the situations where we have exactly one solution, more than one solution and infinitely many solutions for a linear equation in one variable. 

Use the properties of equality to simplify the equation given below. Say whether the equation has one, zero, or infinitely many solutions.

Example 1 :

4x - 3  =  2x + 13

Solution : 

4x - 3  =  2x + 13

Subtract 3x from each side.

2x - 3  =  13

Add 3 to each side. 

2x  =  16

Divide each side by 2.

x  =  8

Justify and Evaluate :

Substitute x = 8 in the given equation. 

4(8) - 3  =  2(8) + 13  ?

32 - 3  =  16 + 13  ?

29  =  29 ------> True

Substitute some other value for x, say x  =  10. 

4(10) - 3  =  2(10) + 13  ?

40 - 3  =  20 + 13  ?

37  =  23  False

Only x = 8 makes the equation a true statement and not any other value. So, there is only one solution, that is x = 8.

Example 2 :

4x - 5  =  2(2x - 1) - 3

Solution : 

4x - 5  =  2(2x - 1) - 3

Use distributive property.

4x - 5  =  2(2x) - 2(1) - 3

Simplify

4x - 5  =  4x - 2 - 3

4x - 5  =  4x - 5

We find the same coefficient for x on both sides.

So, subtract 4x on from each side to get rid of x-terms.

-5  =  -5

When we solve the given equation, we don't find 'x' in the result. But the statement (-5 = -5) we get at last is true. So there are infinitely many solutions.

Example 3 :

4x + 2  =  4x - 5

Solution : 

We find the same coefficient for x on both sides.

So, subtract 4x from each side to get rid of x-terms. 

2  =  -5

When we solve the given equation, we don't find 'x' in the result. But the statement (2 = -5) we get at last is false. So there is no solution. 

Example 4 :

The equation P = 2.5m + 35 represents the price P (in dollars) of a bracelet, where m is the cost of the materials (in dollars). The price of a bracelet is $115. What is the cost of the materials?

Solution : 

p = 2.5m + 35

here p is the bracelet and m is the cost of materials.

Price of bracelet = $115

115 = 2.5m + 35

2.5m = 115 - 35

2.5m = 80

m = 80/2.5

= 32

So, cost of material is $32.

Example 5 :

A 455-foot fence encloses a pasture. What is the length of each side of the pasture?

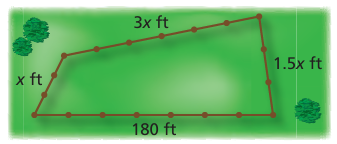
Solution : 

Length of fencing = 455 foot

3x + 1.5x + 180 + x = 455

5.5 x + 180 = 455

5.5x = 455 - 180

5.5x = 275

x = 275/5.5

= 50

3x ==> 3(50) ==> 150 ft

x = 50 ft

1.5x = 1.5(50) ==> 75 ft

Example 6 :

A machine prints 230 movie posters each hour. Write and solve an equation to find the number of hours it takes the machine to print 1265 posters.

Solution : 

Number of movie posters printed = 230 per hour

Let n be the number of hours.

Number of posters printed = 1265

230n = 1265

n = 1265/230

= 5.5

So, the required number of hours is 5.5.

Example 7 :

Use the table to write and solve an equation to find the number of points p you need to score in the fourth game so that the mean number of points is 20?

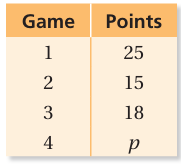
Solution : 

Mean of number of points = 20

(25 + 15 + 18 + p) / 4 = 20

33 + p = 20(4)

33 + p = 80

p = 80 - 33

p = 47

So, the value of p is 47.

Example 8 :

A boat travels x miles per hour upstream on the Mississippi River. On the return trip, the boat travels 2 miles per hour faster. How far does the boat travel upstream?

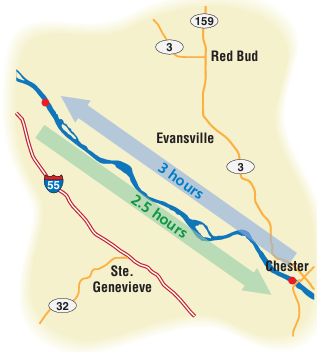
Solution : 

The speed of the boat on the return trip is (x + 2) miles per hour.

Distance of upstream = distance of downstream

3x = 2.5(x + 2)

3x = 2.5x + 5

3x - 2.5x = 5

0.5x = 5

x = 5/0.5

x = 10

The boat travels 10 miles per hour for 3 hours upstream. So, it travels 30 miles upstream.

Example 9 :

One-sixth of the girls and two-sevenths of the boys in a school marching band are in the percussion section. The percussion section has 6 girls and 10 boys. How many students are in the marching band? Explain.

Solution : 

Let g be total number of girls in the class

Let b be total number of boys in the class.

1/6 of g = 6

2/7 of b = 10

Total number of students = number of boys + number of girls 

= 35 + 12

= 47

So, total number of students are 47.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.