HOW TO DETERMINE IF A SEQUENCE IS ARITHMETIC

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

If a sequence is arithmetic, the difference between any two consecutive terms will be same along the sequence.

Let a₁, a₂, a₃, a₄, a₅, a₆, ............ be a sequence.

Let 'd' be the difference between the first term and a₁ and second term a₂. That is,

d = a₂- a₁

In the above sequence, if the difference between any two consecutive terms is 'd' along the sequence, then the sequence is arithmetic.

d₁ = a₂- a₁

d₂ = a₃- a₂

d₃ = a₄- a₃

d₄ = a₅- a₄

d₅ = a₆- a₅

d₁ = d₂ = d₃ = d₄ = d₅ = d

The difference 'd' is called common difference.

Determine whether the following sequences are arithmetic. If so, state the common difference.

Example 1 :

7, 6, 5, 4, ...........

Solution :

d₁ = a₂ - a₁

= 6 - 7

= -1

d₂ = a₃ - a₂

= 5 - 6

= -1

d₃ = a₄ - a₃

= 4 - 5

= -1

d₁ = d₂ = d₃ = -1

The difference between any two consecutive terms is same along the sequence. So, the given sequence is arithmetic.

Example 2 :

10, 12, 15, 18, ...........

Solution :

d₁ = a₂ - a₁

= 12 - 10

= 2

d₂ = a₃ - a₂

= 15 - 12

= 3

d₃ = a₄ - a₃

= 18 - 15

= 3

d₁ ≠ d₂

The difference between any two consecutive terms is not same along the sequence. So, the given sequence is not arithmetic.

Example 3 :

9, 5, -1, -5, ...........

Solution :

d₁ = a₂ - a₁

= 5 - 9

= -4

d₂ = a₃ - a₂

= -1 - 5

= -6

d₃ = a₄ - a₃

= -5 - (-1)

= -5 + 1

= -4

d₁ ≠ d₂

The difference between any two consecutive terms is not same along the sequence. So, the given sequence is not arithmetic.

Example 4 :

-15, -11, -7, -3, ...........

Solution :

d₁ = a₂ - a₁

= -11 - (-15)

= -11 + 15

= 4

d₂ = a₃ - a₂

= -7 - (-11)

= -7 + 11

= 4

d₃ = a₄ - a₃

= -3 - (-7)

= -3 + 7

= 4

d₁ = d₂ = d₃ = 4

The difference between any two consecutive terms is same along the sequence. So, the given sequence is arithmetic.

Example 5 :

-0.3, 0.2, 0.7, 1.2, ...........

Solution :

d₁ = a₂ - a₁

= 0.2 - (-0.3)

= 0.2 + 0.3

= 0.5

d₂ = a₃ - a₂

= 0.7 - 0.2

= 0.5

d₃ = a₄ - a₃

= 1.2 - 0.7

= 0.5

d₁ = d₂ = d₃ = 0.5

The difference between any two consecutive terms is same along the sequence. So, the given sequence is arithmetic.

Example 6 :

2.1, 4.2, 8.4, 17.6, ...........

Solution :

d₁ = a₂ - a₁

= 4.2 - 2.1

= 2.1

d₂ = a₃ - a₂

= 8.4 - 4.2

= 4.2

d₃ = a₄ - a₃

= 17.6 - 8.4

= 9.2

d₁ ≠ d₂

The difference between any two consecutive terms is not same along the sequence. So, the given sequence is not arithmetic.

Example 7 :

Describe and correct the error in finding the common difference of the arithmetic sequence.

Solution :

Common difference :

d₁ = a₂ - a₁

= 1 - 2

-1

d₂ = a₃ - a₂

= 0 - 1

= -1

d₃ = a₄ - a₃

= -1 - 0

= -1

The common difference is -1, but it shows 1 is the common difference. That is the error.

Example 8 :

Describe and correct the error in writing an equation for the nth term of the arithmetic sequence.

Solution :

a = 14, d = 22 - 14 ==> 8

a_n = a + (n - 1) d

= 14 + (n - 1) 8

= 14 + 8n - 8

= 6 + 8n

Example 9 :

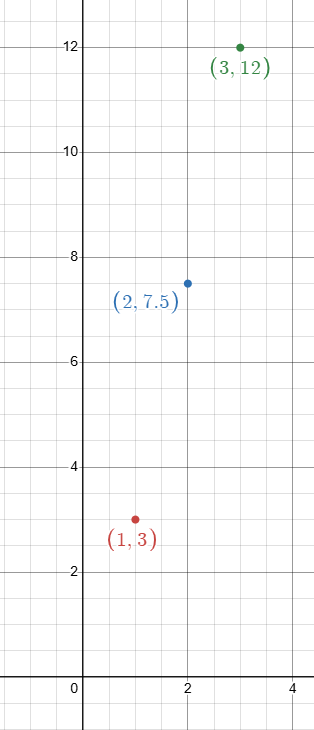
The first term of an arithmetic sequence is 3. The common difference of the sequence is 1.5 times the first term. Write the next three terms of the sequence. Then graph the sequence.

Solution :

First term (a) = 3

Common difference (d) = 1.5a

= 1.5(3)

d = 4.5

3, 3 + 4.5, 7.5 + 4.5, ..............

= 3, 7.5, 12, ...............

Example 10 :

The first row of a dominoes display has 10 dominoes. Each row after the first has two more dominoes than the row before it. Write the first five terms of the sequence that represents the number of dominoes in each row.