PROBLEMS ON SURFACE AREA OF COMBINED SHAPES

Problem 1 : 

A circus tent is in the form of a cylinder with a height of 3 m and conical above it. If the base radius is 52.5 m and the slant height of the cone is 53 m, find the canvas needed to make the tent.

Solution :

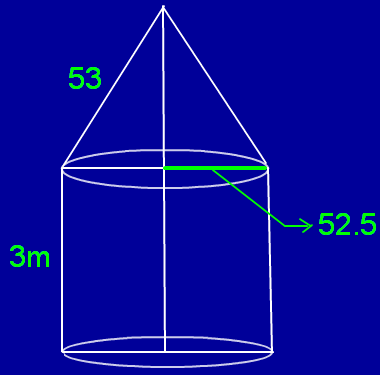
Cylindrical part :

The radius of the cylindrical part (r) = 52.5 m

Height of the cylindrical part(h) = 3 m

Curved surface-area of the cylindrical part = 2πrh

 =  2π(52.5)(3)

=  315 π m²

Conical part:

The radius of the conical part  =  52.5 m

Slant height of the conical part  =  53 m

Curved Surface-area of the conical part  =  πrl

  =  π (52.5) (53)

  =  (2782.5) π

Area of the canvas required :

Area of the canvas required = CSA of the cylindrical part + CSA of the conical part 

  =  315π + (2782.5)π

  =  (3097.5)π m²

Hence, area of the canvas required  =  (3097.5)π m²

Problem 2 :

A vessel is in the form of hollow cylinder which has been surmounted on a hemispherical bowl. The diameter of a hemisphere is 14cm and the total height of a vessel is 13cm. Find the required curved surface area of the vessel.

Solution :

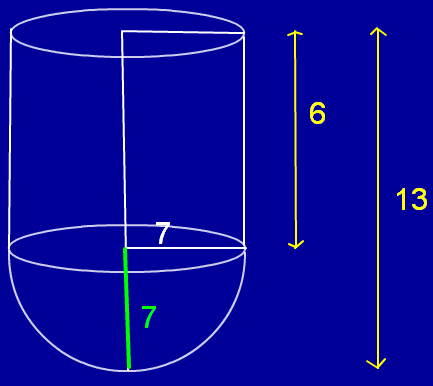
Diameter of the hemisphere  =  14 cm

Radius of the hemisphere  =  14/2  =  7 cm

Radius of the cylinder = radius of the hemisphere  =  7 cm

Total height of the vessel  =  14 cm

Total height of the vessel = height of the cylinder + radius of the hemisphere

13  =  height of the cylinder + 7

Height of the cylinder  =  13 - 7  =  6 cm

Curved Surface Area of the vessel = CSA of the cylinder + CSA of the hemisphere

  =  2πrh + 2πr²

Here r = 7 and h = 6

  =  2π(7)(6) + 2π (7)²

  =  84π + 98π

  = 182π

Hence, the Curved Surface Area of the Vessel = 182 π cm²

Problem 3 :

A play top is in the form of a hemisphere surmounted on a cone. The diameter of the hemisphere is 3.6 cm. The total height of the play top is 4.2 cm. Find its total surface area.

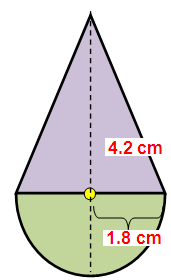
Solution :

Let r and h are radius and height of the cone.

diameter of the hemisphere  =  3.6 cm

radius of hemisphere (r)  =  3.6/2  =  1.8 cm

total height of the play top  =  4.2cm

radius of hemisphere + height of cone = 4.2

1.8 + h  =  4.2

h  =  4.2-1.8

h  =  2.4 cm

Now we are going to find slant height of cone

l²  =  r²+h²

=  (1.8)²+ (2.4)²

=  3.24 + 5.76

l²  =  9

L  =  √(3 ⋅ 3)

L  =  3 cm

To find the total surface area of the play top, we have to find the sum of curved surface area of hemisphere and curved surface area of cone.

Total surface area of play top = C.S.A of hemisphere + C.S.A of cone

=  2Πr²+Πrl

=  Πr(2r+l)

=  Π ⋅ (1.8) [2(1.8) + 3] 

=  Π ⋅ (1.8) (3.6+3) 

=  Π (1.8) (6.6)

=  11.88 Π cm²

Total surface area of the play top = 11.88 Π cm².

Problem 4 :

Yanna celebrated her fifth birthday. She ate at her favorite restaurant. She ordered a soda pop. The soda pop came in a cup shaped like a cylinder with a cone top. The cylinder part of the cup was 6 inches tall and the height of the top was 2 inches. The radius of the cup was 2 inches. What was the surface area of the cup?

Solution :

Surface area of the cup = surface area of cylinder + surface area of cone

= 2 Πrh + Πrl

= Πr(2h + l)

Height of cylinder = 6 inches, height of cone = 2 inches

radius = 2 inches

slant height (l) =  √r² + h²

=  √2² + 2²

= √(4+4)

= √8

= 2 √2 inches

applying these values in the formula, we get

= Π x 2 (2(6) + 2 √2)

= 2Π(12 + 2√2) square inches

Problem 5 :

James wants to paint his grain silo. The diameter of the silo is 8 meters. The height of the cylindrical part is 12 meters. The slant height of the cone top is 4.5 meters.

a. Calculate the surface area of the grain silo.

b. A five-gallon bucket of paint covers 20 square meters. How many buckets of paint will James need?

Solution :

a)  Height of cylinder = 12 m, radius = 8/2 ==> 4 m

Slant height of the cone = 4.5 m

Surface area = surface area of cylinder + surface area of cone

= 2 Πrh + Πrl

= Πr(2h + l)

= 3.14 x 4 (2(12) + 4.5)

= 3.14 x 4(24 + 4.5)

= 12.56(28.5)

= 357.96 square meter

b) 5 gallons of paint can cover = 20 square meter

1 square meters requires = 5/20 gallons

= 1/4 gallons

= 357.96/4

= 89.49 gallons

Approximately 90 gallons of bucket of paint is needed.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.