COTERMINAL ANGLES

One complete rotation of a ray in the counter-clockwise direction results in an angle measuring of 360° or 2π.

By continuing the counter-clockwise rotation, angles larger than 360° can be produced.

If we rotate in clockwise direction, negative angles are produced.

Angles 57°, 417° and -303° have the same initial side and terminal side but with different amount of rotations, such angles are called coterminal angles.

Thus, angles in standard position that have the same terminal sides are coterminal angles . Hence, if α and β are coterminal angles, then

ᵦ = α + k(360°)

or

ᵦ = α + k(2π)

where k is an integer.

The measurements of coterminal angles differ by an integral multiple of 360°.

For example, 417° and -303° are coterminal because

417° - (-303°) = 720° = 2(360°)

Note :

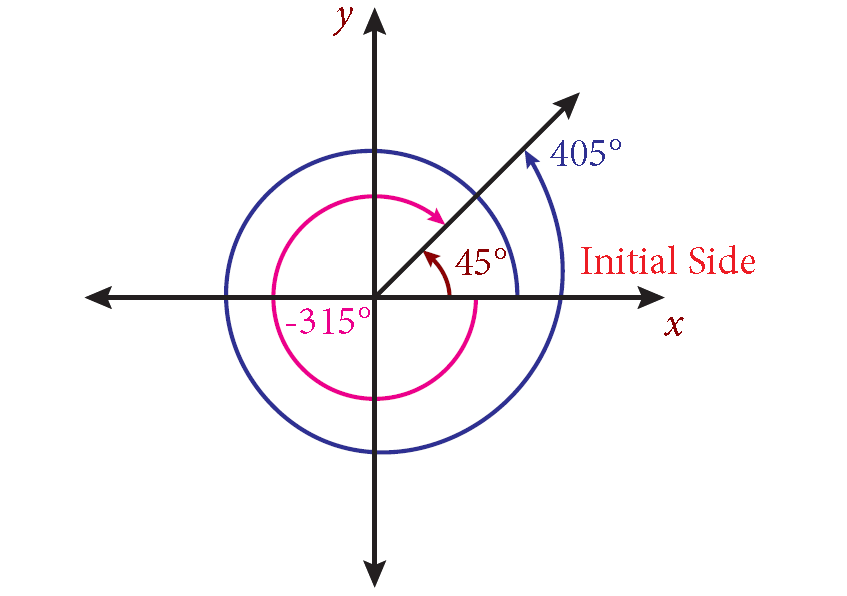
(i) Observe that 45°, −315° and 405° lie in the first quadrant.

(ii) The following pairs of angles are coterminal angles (30°, 390°) ; (280°, 1000°) and (-85°, 275°).

Solved Problems

Problem 1 :

Find a positive and a negative angle that are coterminal with the angle 75°.

Solution :

Positive angle that is coterminal with 75° :

75° + 360° = 435°

So, positive angle that is coterminal with 75° is 435°.

Negative angle that is coterminal with 75° :

75° - 360° = -285°

So, negative angle that is coterminal with 75° is -285°.

Problem 2 :

Find a positive and a negative angle that are coterminal with the angle 2π/3.

Solution :

Positive angle that is coterminal with 2π/3 :

2π/3 + 2π = 2π/3 + 6π/3

2π/3 + 2π = (2π + 6π) / 3

2π/3 + 2π = 8π/3

So, positive angle that is coterminal with 2π/3 is 8π/3.

Negative angle that is coterminal with 2π/3 :

2π/3 - 2π = 2π/3 - 6π/3

2π/3 - 2π = (2π - 6π) / 3

2π/3 - 2π = -4π/3

So, negative angle that is coterminal with 2π/3 is -4π/3.

Problem 3 :

Find a positive and a negative angle that are coterminal with the angle -200°.

Solution :

Positive angle that is coterminal with -200° :

-200° + 360° = 160°

So, positive angle that is coterminal with -200° is 160°.

Negative angle that is coterminal with -200° :

-200° - 360° = -560°

So, negative angle that is coterminal with -200° is -560°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.