CONGRUENT FIGURES

Example 1 :

Identify a sequence of transformations that will transform figure X into figure Y.

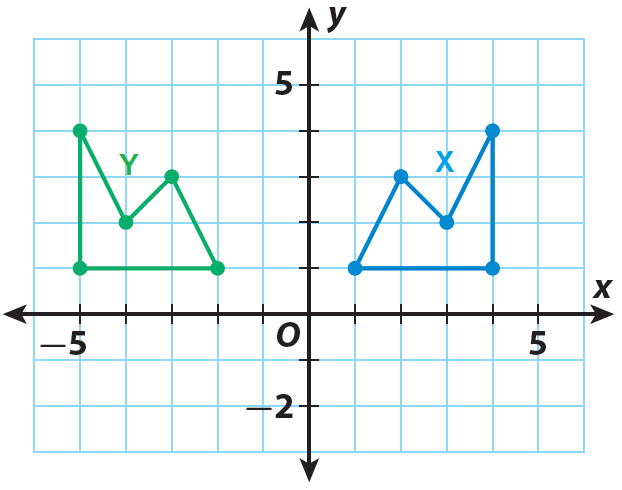
Solution :

To transform figure X into figure Y, you need to reflect it over the y-axis and translate one unit to the left. A sequence of transformations that will accomplish this is

(x, y) → (-x, y) and (x, y) → (x - 1, y)

Example 2 :

Identify a sequence of transformations that will transform figure A into figure B.

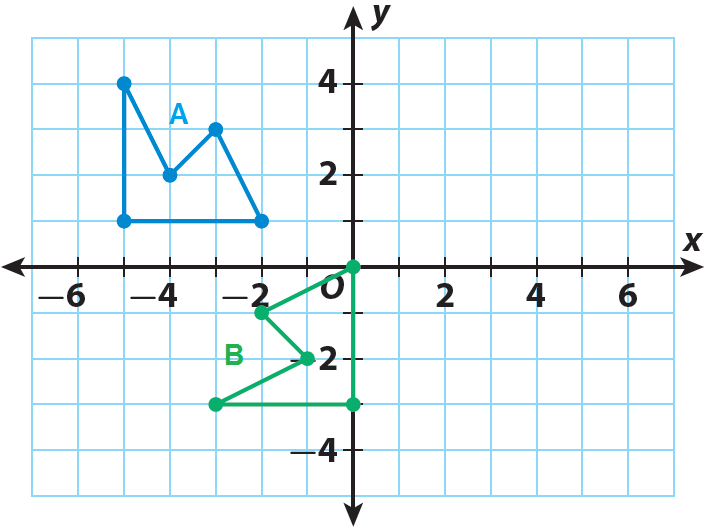
Solution :

Any sequence of transformations that changes figure A into figure B will need to include a rotation. A 90° counterclockwise rotation about the origin would properly orient figure A, but not locate it in the same position as figure B.

The rotated figure would be 2 units below and 1 unit to the left of where figure B is. We would need to translate the rotated figure up 2 units and right 1 unit.

A sequence of transformations is a 90° counterclockwise rotation about the origin,

(x, y) → (-y, x), followed by (x, y) → (x + 1, y + 2)

Example 3 :

Identify a sequence of transformations that will transform figure P into figure Q.

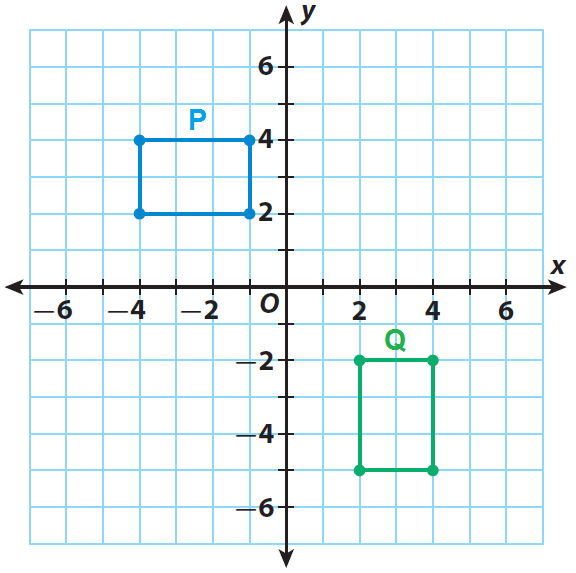
Solution :

A sequence of transformations that changes figure P to figure Q will need to include a rotation. A 90º clockwise rotation around the origin would result in the figure being oriented as figure Q.

However, the rotated figure would be 6 units above where figure Q is. We would need to translate the rotated figure down 6 units.

A sequence of transformations is a 90º clockwise rotation about the origin,

(x, y) → (y, -x), followed by (x, y) → (x, y - 6)

Example 4 :

Identify a sequence of transformations that will transform figure A into figure B.

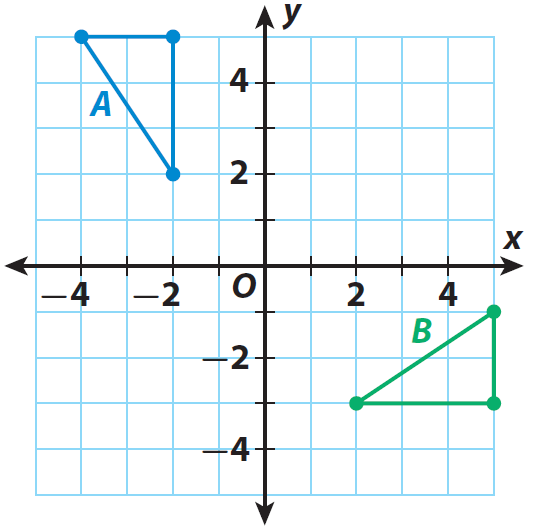
Solution :

Rotation 90° clockwise about origin, translation 5 units down.

(x, y) → (y, -x), (x, y) → (x, y - 5)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.