POINT OF CONCURRENCY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We know that two non parallel lines intersect at a point. If a third line is drawn passing through the same point, these straight lines are called concurrent-lines.
In the figure shown below, the straight lines AB, CD and EF are passing through one point P.
So, the point P is the point of concurrency.
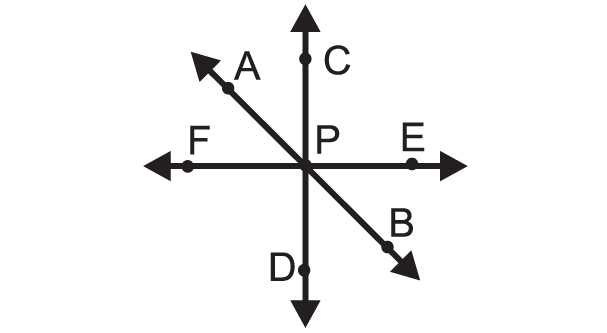
Example 1 :
In the figure shown below, find the concurrent lines and point of concurrency.
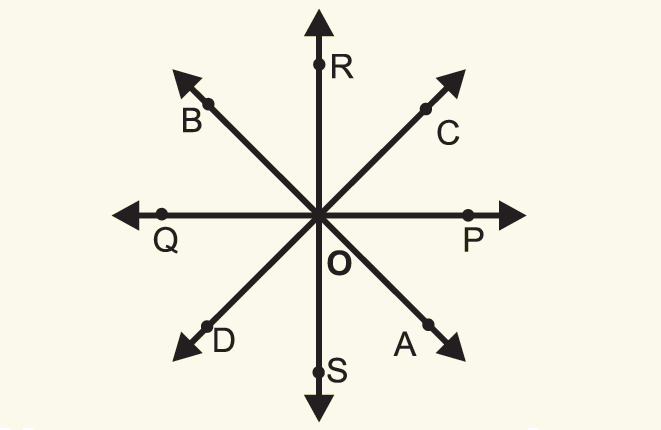
Solution :
In the diagram above, since the straight lines AB, CD, PQ and RS are all meeting at the same point O, they are concurrent line.
The point of concurrency is O.
Example 2 :
Prove that the following lines are concurrent and find the point of concurrency.
3x - 4y + 5 = 0
7x - 8y + 5 = 0
4x + 5y = 45
Solution :
3x - 4y + 5 = 0 ----A
7x - 8y + 5 = 0 ----B
4x + 5y - 45 = 0 ----C
Solve A and B :
B - 2A ----> x - 5 = 0
x = 5
Substitute x = 5 in (1).
3(5) - 4y + 5 = 0
15 - 4y + 5 = 0
20 - 4y = 0
-4y = -20
y = 5
The point of intersection of A and B is (5, 5).
Now, check whether the line C satisfies the point (5, 5).
Substitute x = 5 and y = 5 in C,
4(5) + 5(5) = 45 (true ?)
20 + 25 = 45 (true ?)
45 = 45 (yes, it is true)
Point of intersection of lines A and B satisfies the third line.
Therefore, all the three lines A, B and C are intersecting at the same point (5, 5) and they are concurrent.
The point of concurrency is (5, 5).
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 41)
Dec 28, 25 06:05 PM
10 Hard SAT Math Questions (Part - 41)

