COMPARE AND ORDER INTEGERS

We use number line to compare and order integers.

That is,  if we want to compare two integers, first we have to locate the integers on the number line and mark them. 

The integer which comes to the right of the other integer is greater. The integer which comes to the left of the other integer is smaller. 

To order the integers, we have to locate the given integers on the number line and mark them. Then, write the integers from left to right to list them in order from least to greatest.  

Comparing Integers

Example 1 :

Compare the integers -4 and 4.

Solution :

Let us locate the two integers -4 and 4 on a number line and mark them. 

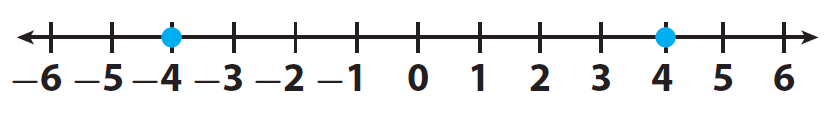
Here, the positive integer 4 comes to the right of -4.

Therefore 4 is greater than -4.

And -4 comes to the left of 4.  

Therefore -4 is smaller than 4.

Example 2 :

Compare the integers -1 and 1.

Solution :

Let us locate the two integers -1 and 1 on a number line and mark them.

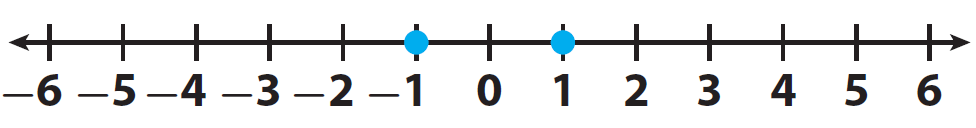
Here, the positive integer 1 comes to the right of -1.

Therefore 1 is greater than -1.

And -1 comes to the left of 1.  

Therefore -1 is smaller than 1.

Ordering Integers

Example 3 :

Order the integers -2, -5, 4, 0, -3, -1, 3 from least to greatest.

Solution :

Let us locate the integers -2, -5, 4, 0, -3, -1, 3 on a number line and mark them.

From the above number line, write the integers from left to right to list them in order from least to greatest.  

Thus, we get

-5, -3, -2, -1, 0, 3, 4

Solving Word Problems

Example 4 :

In 2010, Sacramento, California, received 23 inches in annual precipitation. In 2011, the city received 17 inches in annual precipitation. In which year was there more precipitation ?

Solution :

Locate the two integers 23 and 17 on a number line and mark them.

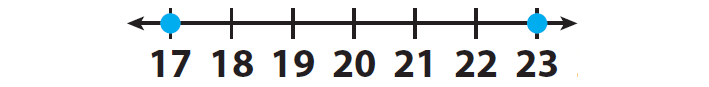
23 is to the right of 17 on the number line.

This means that 23 is greater than 17.

We can write the above situation in terms of inequality as 23 > 17.

17 is to the left of 23 on the number line.

This means that 17 is less than 23.

We can write the above situation in terms of inequality as 17 < 23.

There was more precipitation in 2010.

Example 5 :

John recorded the following golf scores during his first week at a golf academy. Negative numbers represent scores below par, a standard score. In golf, a lower score beats a higher score.

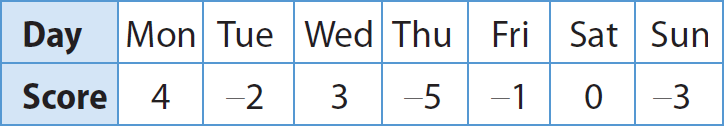
Graph John’s scores on the number line, and then list the numbers in order from least to greatest.

Solution :

Step 1 :

Graph the scores on the number line.

Step 2 :

Read from left to right to list the scores in order from least to greatest.

The scores listed from least to greatest are

–5, –3, –2, –1, 0, 3, 4.

Example 6 :

Show -1 and 6 on a number line and write a sentence comparing their size.

Solution :

-1 is lesser than 6.

Example 7 :

Write the statement 2 > -5 in words, then state whether it is true or false.

Solution :

2 is greater than -5. Always negative numbers are lesser than positive numbers.

Example 8 :

The table shows the highest and lowest elevations for five states.

a. Order the states by their highest elevations, from least to greatest.

b. Order the states by their lowest elevations, from least to greatest.

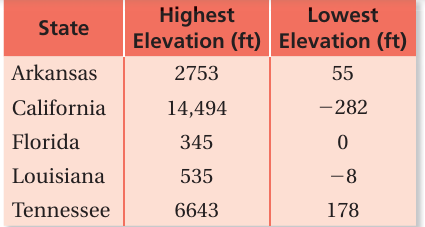
Solution :

a) Highest elevations from least to greatest :

345, 535, 2753, 6643, 14494

Florida, Louisiana, Arkanas, Tennessee, California

b) Lowest elevations from least to greatest :

-282, -8, 0, 55, 178

California,  Louisiana, Florida, Arkanas, Tennessee

Example 9 :

Tell whether the statement is always, sometimes, or never true. Explain.

a)  A positive integer is greater than its opposite.

b)  An integer is less than its opposite and greater than 0.

c)  The median of a set of integers is negative.

Solution :

a)  For example, positive integer 10 

Opposite of 10 is -10

10 is greater than -10.

A positive integer is greater than its opposite. So, it is always true.

b)  

• Let the integer be positive and its opposite will be negative. Then positive number is always greater than the negative number and it is greater than 0.
• Let the integer be negative and its opposite will be positive. Then negative number will not be greater than the positive number.

So, this statement will be sometimes true.

c)  The median of set of integers is 0. So, it will become never true.

Example 10 :

The freezing temperature of nitrogen is − 210°C and the freezing temperature of oxygen is − 223°C. Which has a lower freezing temperature ?

Solution :

Freezing temperature of nitrogen = − 210°C

Freezing temperature of oxygen = − 223°C

-223°C < -210°C

Freezing temperature of oxygen < Freezing temperature of nitrogen

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.