CIRCLES CALCULATE AREA CIRCUMFERENCE RADIUS AND DIAMETER

Radius :

The radius is a line segment with one end point at the center and the other end on the circle. It is denoted by ‘r’.

Diameter :

Diameter is a chord passing through the center of the circle. It is denoted by ‘d’.

The diameter is the longest chord. It is twice the radius.(i.e. d = 2r)

Circumference :

Can we find the distance covered by an athlete if he takes two rounds on a circular track. Since it is a circular track, we cannot use the ruler to find out the distance.

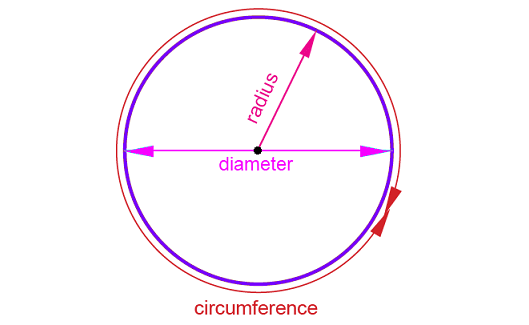
The distance around a circle is called the circumference of the circle, which is denoted by ‘C’.

Circumference of circle = 2πr

Area of circle :

The area of a circle is the number of square units inside that circle

Area of circle = πr²

Example 1 :

Find the circumference of a circle whose diameter is 21 cm.

Solution :

Diameter  =  21 cm

Radius  =  21/2 = 10.5 cm

Circumference of circle  =  2 π r

  =  2 (22/7) x 10.5

  =  44 x 1.5

  =  66 cm

Hence the circumference of circle is 66 cm.

Example 2 :

A wire of length 88 cm is bent as a circle. What is the radius of the circle?

Solution :

Length of the wire  =  circumference of the circle

2 π r  =  88 cm

2 x (22/7) x r  =  88

r  =  (88 x 7)/(2 x 22)

r  =  14 cm

Hence the radius of the circle is 14 cm

Example 3 :

The diameter of a bicycle wheel is 63 cm. How much distance will it cover in 20 revolutions?

Solution :

When a wheel makes one complete revolutions,

Distance covered in one rotation = Circumference of wheel

Circumference of the wheel = 2πr units 

=  2 x (22/7) x (63/2) cm

=  22 x 9  =  198 cm

For one revolution, the distance covered = 198 cm

For 20 revolutions, the distance covered = 20 × 198 cm

=  3960 cm

=  39 m 60 cm [100 cm = 1 m]

Hence the distance covered in 20 revolution is 39 m 60 cm

Example 4 :

A scooter wheel makes 50 revolutions to cover a distance of 8800 cm. Find the radius of the wheel.

Solution :

Distance travelled 

  =  Number of revolutions/Circumference

2πr  =  8800/50

2πr  =  176

2 x (22/7) x r  =  176

r  =  176 x (7/22) x (1/2)

r  =  28 cm

Hence the radius of the wheel is 28 cm

Example 5 :

The radius of a cart wheel is 70 cm. How many revolution does it make in travelling a distance of 132 m?

Solution :

Given: r = 70 cm, Distance travelled = 132 m.

Circumference of a cart wheel = 2πr

= 2 x (22/7) x 70

= 440 cm

Distance travelled

= Number of revolutions x  Circumference

Number of revolutions

  = Distance travelled/Circumference

  =  132 m/440 cm

  =  13200/440

  =  30

Hence the number of revolution is 30.

Example 6 :

A lawn sprinkler sprays water onto part of a circular region, as shown below.

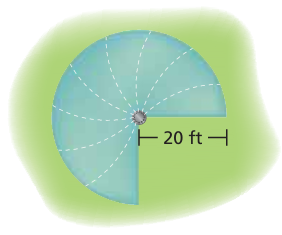
Part A :  What is the area, in square feet, of the region that the sprinkler sprays with water? Show your work and explain your reasoning. (Use 3.14 for π)

Part B : What is the perimeter, in feet, of the region that the sprinkler sprays with water? Show your work and explain your reasoning. (Use 3.14 for π .)

Solution :

a) Area of region that sprinkle sprays with water =

Area of semicircle + area of quarter circle

= (1/2) πr² + (1/4) πr²

= (3/4) πr² 

Radius = 20 ft

= (3/4) x 3.14 x 20² 

= 942 square feet

b) Perimeter of the region

= Circumference of semicircle + circumference of quarter circle

= πr + (1/2) πr

= (3/2)πr

= (3/2) x 3.14 x 20

= 94.2 feet

Example 7 :

A desktop is shaped like a semicircle with a diameter of 28 inches. What is the area of the desktop?

Solution :

Diameter = 28 inches

radius = 14 inches

Area of the semicircle desktop = (1/2)πr²

= (1/2) x 3.14 x 14²

= 0.5 x 3.14 x 196

= 307.72 square inches

Example 8 :

The circular rug is placed on a square floor. The rug touches all four walls. How much of the floor space is not covered by the rug?

Solution :

Diameter = 14 ft

Radius = 7 ft

Area of circular rug = πr²

= 3.14 x 7²

= 3.14 x 49

= 153.86 square ft

Example 9 :

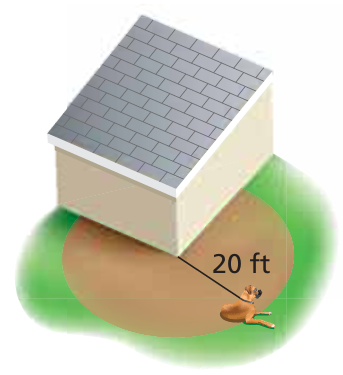
A dog is leashed to the corner of a house. How much running area does the dog have? Explain how you found your answer.

Solution :

Area covered by the dog = (3/4) of area of circle

radius = 20 ft

= (3/4) πr²

= 0.75 x 3.14 x 20² 

= 942 square feet

Example 10 :

Is the area of a semicircle with a diameter of x greater than, less than, or equal to the area of a circle with a diameter of (1/2)  x ? Explain.

Solution :

Diameter of semicircle = x

Radius of semicircle = x/2

Area of semicircle = (1/2) πr²

= (1/2) ⋅ 3.14 ⋅ (x/2)²

= 0.5 ⋅ 3.14 ⋅ (x/4)

= 0.3925x

Radius of circle = (x/2)/2

= x/4

Area of semicircle = (1/2) πr²

= (1/2) ⋅ 3.14 ⋅ (x/4)²

= 0.5 ⋅ 3.14 ⋅ (x/16)

= 0.098125 x

Area of semicircle is greater.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.