CHECK IF THE FUNCTION IS INCREASING IN THE GIVEN INTERVAL

A function f is said to be increasing function on an interval I if f (x₁) ≤ f (x₂) when x₁ < x₂ in I.

How to find whether the given function is increasing in the given interval.

Step 1 :

Find the first derivative. 

Step 2 :

Apply random values from the given interval. If the simplified value be positive then we can say the given function is increasing. If it is negative we can say the given function is decreasing.

Example 1 :

Check whether y = x² is increasing on the interval (0,∞).

Solution :

As per the procedure first let us find the first derivative.

dy/dx  =  2 x

f'(x)  =  2x

Now let us apply random values from the given interval.

x  =  2 ∈ (0,∞)

f'(2)  =  2(2)

                  =  4 > 0

x  =  6 ∈ (0,∞)

f'(6)  =  2(6)

=  12 > 0

So the given function is increasing in the interval (0,∞).

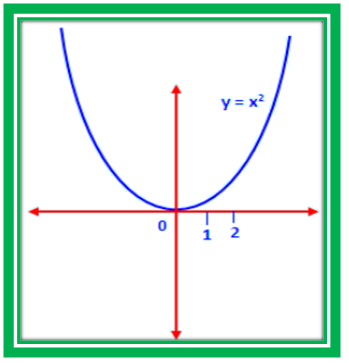
Example 2 :

Check whether y = sin x is increasing on the interval (0, Π/2).

Solution :

As per the procedure first let us find the first derivative.

dy/dx  =  cos x 

f'(x)  =  cos x 

Now let us apply random values from the given interval

x  =  Π/3 ∈ (0,Π/2)

f'(Π/3)  =  cos Π/3

  =  1/2 > 0

x  =  Π/6 ∈ (0,Π/2)

  f'(Π/6)  =  cos Π/6

  =  √3/2 > 0  

So, the given function is increasing in the interval (0, Π/2).

Example 3 :

Check whether y  =  2x³+x²-20x is increasing on the interval (-∞, -2).

Solution :

As per the procedure first let us find the first derivative

f'(x)  =  6x² + 2x

Now let us apply random values from the given interval

x  =  -5 ∈ (-∞, -2)

f'(-5)  =  6(-5)² + 2(-5)

  =  6(25) -10

  =  150 - 10

  =  140 > 0 

x  =  -3 ∈ (-∞, -2)

 f'(-3)  =  6(-3)² + 2(-3)

  =  54 - 6

  =  48 > 0

So the given function is increasing in the interval (-∞,-2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.