CHECK IF POINT ARE ON THE SAME LINE WORKSHEET

Problem 1 :

Does (3, -2) lie on the line with equation 5x-2y  =  20 ?

Problem  2 :

Does (3, 4) lie on the line with equation 3x-2y = 1 ?

Problem 3 :

Find k, if 

(a)  (3, 4) lies on the line with equation 3x-2y = k

(b)  (-1, 3) lies on the line with equation 5x-2y  =  k

Problem 4 :

Find a given that :

(a)  (a, 3) lies on the line with equation y  =  2x-1

(b)  (-2, a) lies on the line with equation y  =  1-3x

Problem 5 :

In which pairs of coordinates is the y-value 7 more than the x-value?

a) (1, 8)     b) (3/2, 8  1/2)     c)  (3.1, 3.8)

d)  (19/7, 26/7)

Problem 6 :

Which of the points lie on the line y = x – 5? 

a)  (3, 8)   b)  (2, -3)     c)  (3.7, 3.2)   d)  (a, a - 5)

Problem 7 :

Show that the point (–12, 61) lies on the line 6y = 3x + 402

Problem 8 :

The equation of line L2 is 4y + 16 = 12x.

a) Write the equation of L2 in the form y = mx + c

b) Draw the graph of L2 on the grid.

c) Does the point (2, 9) lie on, above or below L2?

Problem 9 :

The equation of L1 is given by 2y – 12x = 17

a) Write the equation of L1 in the form y = mx + c.

b) Does L1 pass through the point ( 1 2 , 12)? Show workings to justify your answer.

Problem 10 :

Show that the point (–9, 7) does not lie on the line

y = 2 – x

Problem 11 :

Does the point (13, –5) lie on the line y = 8 – x?

1) Solution :

By applying the given point (3, -2) into the given equation, we get

5(3)-2(-2)  =  20

15 + 4  =  20

19  =  20

Since the given point doesn't satisfy the given equation. we say that the given point is not on the straight line.

2) Solution :

By applying the given point in the equation of the line, we get

3(3)-2(4)  =  1

9-8  =  1

1  =  1

Since the given point satisfies the equation, the given point lies on the line.

3) Solution :

(a)  Since the given (3, 4) lies on the given line, it will satisfy the equation.

x  =  3 and y  =  4

3(3)-2(4)  =  k

9-8  =  k

k  =  1

So, the value of k is 1.

(b)  Since the given (-1, 3) lies on the given line, it will satisfy the equation.

x  =  -1 and y  =  3

5(-1)-2(3)  =  k

-5-6  =  k

k  =  -11

So, the value of k is -11.

4) Solution :

Since the given point (a, 3) lies on the line y = 2x-1, the point will satisfy the equation.

Here x  =  a and y  =  -3

-3  =  2a-1

-3+1  =  2a

2a  =  -2

a  =  -1

So, the value of a is -1.

(b)  (-2, a) lies on the line with equation y  =  1-3x

Since the given point (-2, a) lies on the line y = 1-3x, the point will satisfy the equation.

Here x  =  -2 and y  =  a

a  =  1-3(a)

a  =  1-3a

a+3a  =  1

4a  =  1

a  =  1/4

So, the value of a is 1/4.

5) Solution :

In which pairs of coordinates is the y-value 7 more than the x-value?

a) (1, 8)     b) (3/2, 8  1/2)     c)  (3.1, 3.8)

d)  (19/7, 26/7)

Option a :

(1, 8)

x = 1, y = 8 ==> 1 + 7 (True)

Option b :

(3/2, 8  1/2)

x = 3/2, y = 8  1/2

y = 3/2 + 7

= (3 + 14)/2

= 17/2

y = 8  1/2 (True)

Option c :

(3.1, 3.8)

x = 3.1, y = 3.8

y = 3.1 + 7

10.1 ≠ 3.8 (False)

Option d :

(19/7, 26/7)

x = 19/7, y = 26/7

y = 19/7 + 7

= (19 + 49)/7

= 68/77 (False)

So, options a and b are correct.

6) Solution :

Which of the points lie on the line y = x – 5? 

a)  (3, 8)   b)  (2, -3)     c)  (3.7, 3.2)   d)  (a, a - 5)

Option a :

(3, 8)

y = x – 5

8 = 3 - 5

8 = -2 (False)

Option b :

(2, -3)

y = x – 5

-3 = 2 - 5

-3 = -3 (True)

Option c :

(3.7, 3.2)

y = x – 5

3.2 = 3.7 - 5

3.2 = -1.3 (False)

Option d :

(a, a - 5)

y = x – 5

a - 5 = a - 5 (True)

Options b and d are correct.

7) Solution :

To check if the point (-12, 61) lies on the line 6y = 3x + 402, we have to apply the point in the line.

6(61) = 3(-12) + 402

366 = -36+ 402

366 = 366

So, the point lies on the line.

8) Solution :

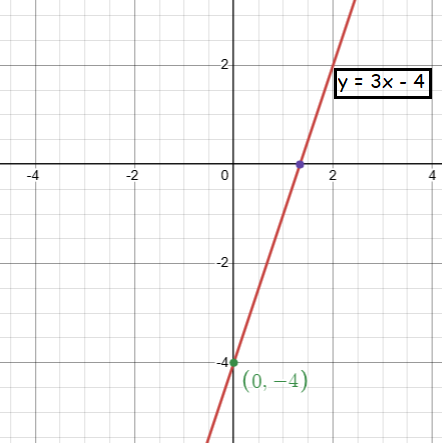
The equation of line L2 is 4y + 16 = 12x.

4y = 12 x - 16

y = (12x - 16)/4

y = 3x - 4

b) Draw the graph of L2 on the grid.

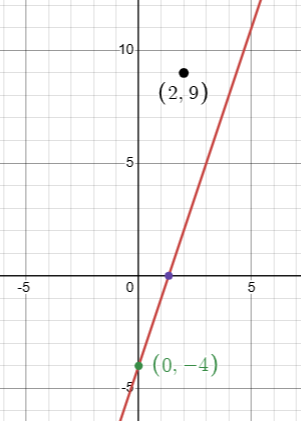
c) When x = 2, y = 9

Applying these values in the equation, we get

y = 3x - 4

9 = 3(2) - 4

9 = 6 - 4

9 > 2

So, the point (2, 9) will lie above the line.

9) Solution :

2y – 12x = 17

a) 2y = 12x + 17

Dividing by 2 on both sides.

y = 12x/2 + (17/2)

y = 6x + (17/2)

b) When x = 1/2, y = 12

12 = 6(1/2) + (17/2)

12 = 3 + (17/2)

Since they are not equal, the point (1/2, 12) does not lie on the line.

10) Solution :

Show that the point (–9, 7) does not lie on the line

y = 2 – x

When x = -9 and y = 7

7 = 2 - (-9)

7 = 2 + 9

7 ≠ 11

So, the point does not lie on the line.

11) Solution :

Does the point (13, –5) lie on the line y = 8 – x?

When x = 13, y = -5

-5 = 8 - 13

-5 = -5

So, the point lies on the line.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.