CENTRAL ANGLES AND ARC MEASURES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. A central angle is an angle with its vertex at the center of the circle and its two sides are radii.
2. For example : m∠POQ is a central angle in circle P shown below.
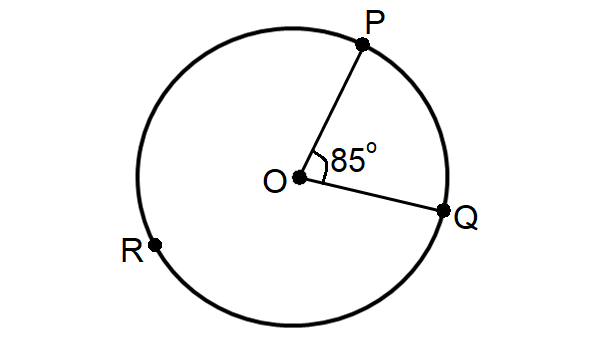
3. The sum of all central angle is 360°.
4. The measure of the arc formed by the endpoints of a central angle is equal to the degree of the central angle.
In the above diagram,
m∠arc PQ = 85°
m∠arc PRQ = 360° - 85° = 275°
5. The measure of the arc formed by the endpoints of the diameter is equal to 180°.
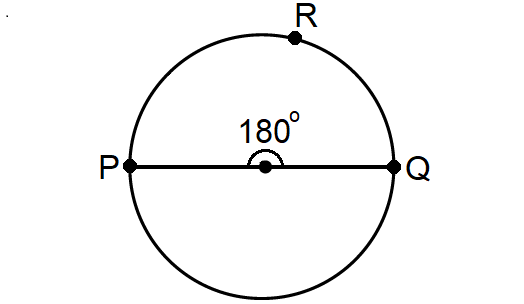
In the above diagram,
m∠arc PRQ = 180°
Example 1 :
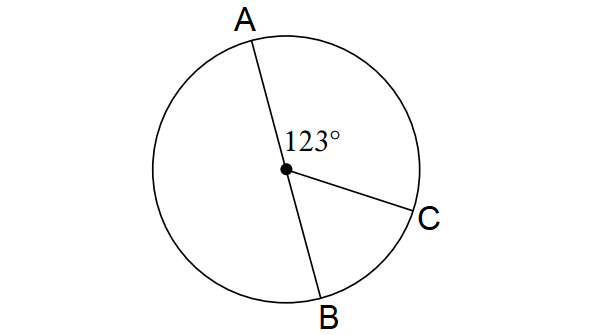
From the diagram shown above, find the following arc measures.
(i) m∠arc BC
(ii) m∠arc ABC
Solution :
(i) m∠arc BC :
AB is the diameter of the above circle.
m∠arc AB = 180°
m∠arc BC + m∠arc CA = 180°
m∠arc BC + 123° = 180°
m∠arc BC = 57°
(ii) m∠arc ABC :
m∠arc ABC = m∠arc AB + m∠arc BC
= 180° + 57°
= 237°
Example 2 :
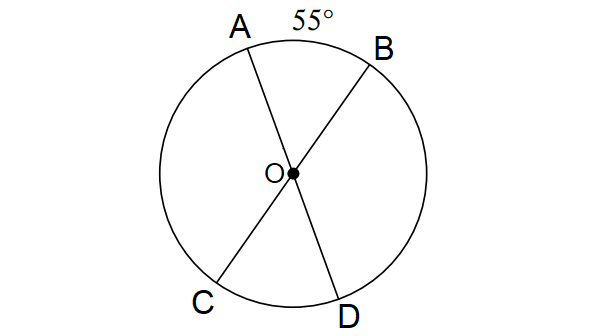
From the diagram shown above, find the following measures.
(i) m∠arc CD
(ii) m∠AOC
(iii) m∠arc BD
(iv) m∠arc ABC
(v) m∠arc CBD
Solution :
(i) m∠arc CD :
m∠AOB and m∠COD are vertical angles.
m∠COD = m∠AOB
m∠arc CD = m∠arc AB
m∠arc CD = 55°
(ii) m∠AOC :
BC is the diameter of the above circle.
m∠arc BAC = 180°
m∠arc BA + m∠arc AC = 180°.
55° + m∠arc AC = 180°.
m∠arc AC = 125°.
m∠AOC = 125°.
(iii) m∠arc BD :
m∠BOD and m∠AOC are vertical angles.
m∠BOD = m∠AOC
m∠BOD = 125°
m∠arc BD = 125°
(iv) m∠arc ABC :
m∠arc ABC = m∠arc ABD + m∠arc DC
= 180° + 55°
= 235°
(v) m∠arc CBD :
m∠arc CBD = m∠arc CAB + m∠arc BD
= 180° + 125°
= 305°
Example 3 :
Find the value of x in the diagram shown below.
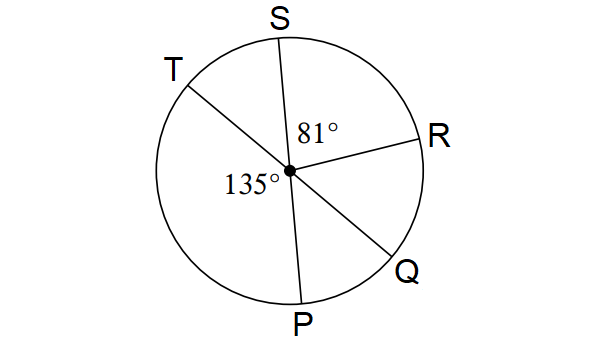
From the diagram shown above, find the m∠arc QTR.
Solution :
Find m∠arc QP :
PS is the diameter of the above circle.
m∠arc PTS = 180°
m∠arc PT + m∠arc TS = 180°
135° + m∠arc TS = 180°
m∠arc TS = 45°
Find m∠arc QTR :
m∠QTR = m∠arc QT + m∠arc TS + m∠arc SR
= 180° + 45° + 81°
= 306°
Example 4 :
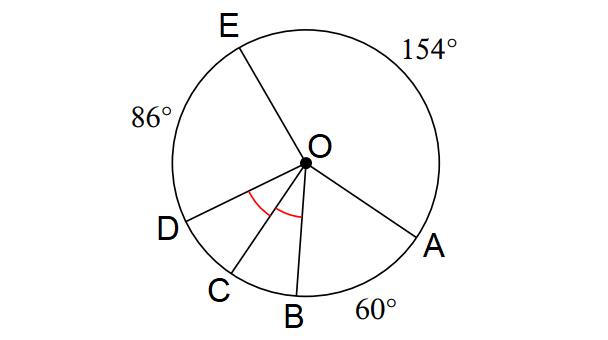
From the diagram shown above, find the following measures.
m∠BOD, m∠BOE and m∠BOC
Solution :
Find m∠BOD :
In the circle above,
m∠arc AB + m∠arc BCD + m∠arc DE + m∠arc EA = 360°
60° + m∠arc BCD + 86° + 154° = 360°
m∠arc BCD + 300° = 360°
m∠arc BCD = 60°
m∠BOD = 60°
Find m∠BOE :
m∠BOE = m∠arc BCD + m∠arc DE
= 60° + 86°
= 146°
Find m∠BOC :
In the above diagram, m∠BOC = m∠COD.
m∠BOC + m∠COD = m∠BOD
m∠BOC + m∠BOC = m∠BOD
2m∠BOC = 60°
m∠BOC = 30°
Example 5 :
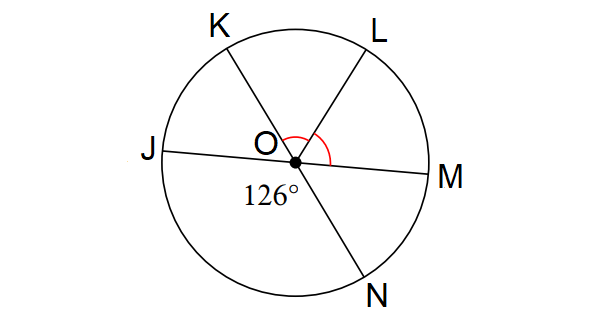
From the diagram shown above, find the following measures.
m∠KOL and m∠arc MNK
Solution :
In the diagram above, m∠JON and ∠KOM are vertical angles.
m∠KOM = m∠KOM
m∠KOM = 126°
m∠KOL + m∠LOM = 126°
In the above diagram, m∠KOL = m∠LOM.
m∠KOL + m∠KOL = 126°
2m∠KOL = 126°
m∠KOL = 63°
Find m∠arc MNK :
m∠arc MNK = 360° - m∠arc KLM
m∠arc MNK = 360° - m∠KOM
m∠arc MNK = 360° - 126°
m∠arc MNK = 234°
Example 6 :
Find the measure of each arc.
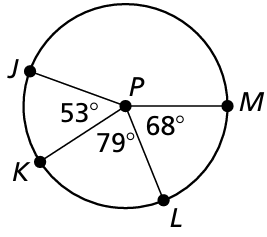
Find the arc measures of following :
a) JL
b) KM
c) JLM
d) JM
Solution :
a)
m∠arc JL = m∠arc JK + m∠arc KL
= 53 + 79
m∠arc JL = 132
b)
m∠KM = m∠arc KL + m∠arc LM
= 79 + 68
m∠KM = 147
c)
m∠JLM = m∠arc JK + m∠arc KL + m∠arc LM
= 53 + 79 + 68
= 200
d)
m∠JM = 360 - m∠arc JLM
= 360 - 200
= 160
Example 7 :
In the circle K is the center. Find the measure of arc DE and arc BA
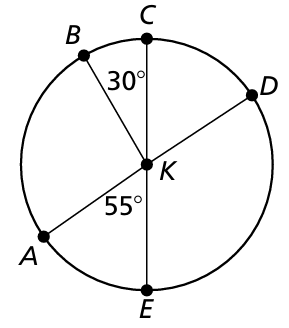
Solution :
m∠arc BC = 30
m∠arc BA = ?
m∠arc AE = 55
m∠arc BC + m∠arc BA + m∠arc AE = 180
30 + m∠arc BA + 55 = 180
m∠arc BA = 180 - 85
m∠arc BA = 95
m∠arc DE + m∠arc AE = 180
m∠arc DE + 55 = 180
m∠arc DE = 180 - 55
m∠arc DE = 125
Example 8 :
A recent survey asked teenagers whether they would rather meet a famous musician, athlete, actor, inventor, or other person. The circle graph shows the results. Find the indicated arc measures.
a) m∠arc AC
b) m∠arc ACD
c) m∠arc ADC
d) m∠arc EBD
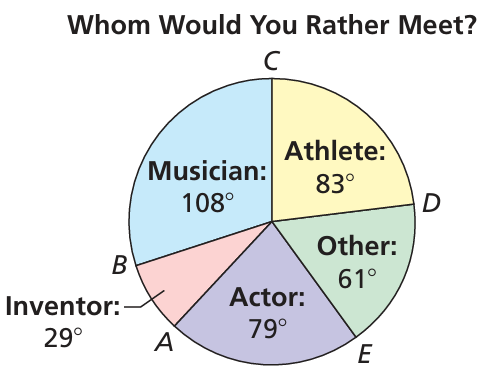
Solution :
a) m∠arc AC = m∠arc CB + m∠arc BA
= 108 + 29
= 137
b) m∠arc ACD = m∠arc AC + m∠arc DC
= 137 + 83
= 220
c) m∠arc ADC = m∠arc AE + m∠arc ED + m∠arc DC
= 79 + 61 + 83
= 223
d) m∠arc EBD = 360 - m∠arc DE
= 360 - 61
= 299
Example 9 :
Find the value of x. Then find the measure of arc AB
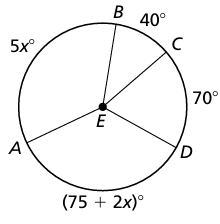
Solution :
m∠arc AB + m∠arc BC + m∠arc CD + m∠arc DA = 360
5x + 40 + 70 + 75 + 2x = 360
185 + 7x = 360
7x = 360 - 185
7x = 175
x = 25
m∠arc AB = 5x
= 5(25)
= 125
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


