AREA OF RHOMBUS WORKSHEET

1. If the lengths of the diagonals of a rhombus are  16 cm and 30 cm, find its area.

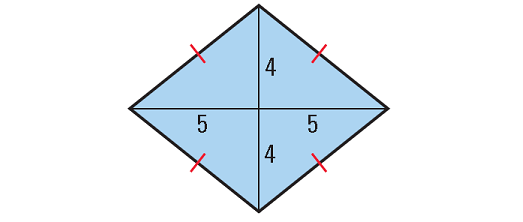
2. Find the area of the rhombus shown below.

3. Area of a rhombus is 192 square cm. If the length of one of the diagonals is 16 cm, find the length of the other diagonal.

4. Area of a rhombus is 120 square units. If the lengths of the diagonals are 10 units and (7x + 3) units, then find the value of x.

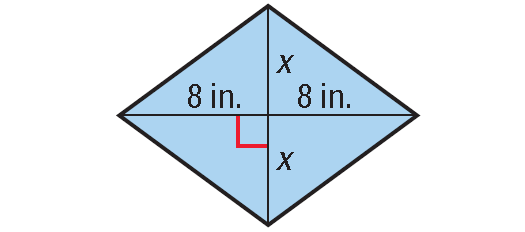
5. Area of the rhombus shown below is 48 square inches. What is the value of x ?

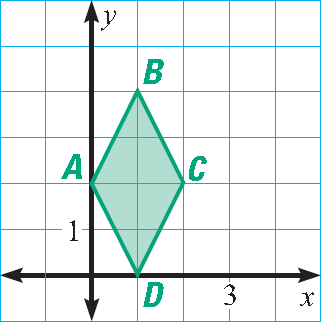
6. Find the area of the rhombus shown below.

7. Find the area of the rhombus having each side equal to 17 cm and one of its diagonals equal to 16 cm.

8.  The area of a rhombus is 150 cm². Thelength of one of its diagonal is 10 cm. The length of the other diagonal is 

a)  25 cm    b)  30 cm     c) 35 cm     d)  40 cm

9. One of the diagonals of a rhombus is double the other diaognal, Its area is 25 sq.cm The sum of the diagonal is :

a)  10 cm   b)  12 cm      c)  15 cm     d)  16 cm

10. The pereimeter of the rhombus is 56 m and its height is 5 m. Its area is 

a)  64 sq.cm  b) 70 sq.cm      c)  78 sq.cm     d)  84 sq.cm

1. Answer :

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 16 for d₁ and 30 for d₂.

=   1/2 ⋅ (16 ⋅ 30)

=   8 ⋅ 30

=  240 cm²

So, area of the rhombus is 240 square cm.

2. Answer :

In the rhombus shown above,

d₁  =  5 + 5  =  10 units

d₂  =  4 + 4  =  8 units

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 10 for d₁ and 8 for d₂.

=   1/2 ⋅ (10 ⋅ 8)

=   5 ⋅ 8

=  40

So, area of the rhombus is 40 square units.

3. Answer :

Area of the rhombus  =  192 cm²

1/2 ⋅ (d₁d₂)  =  192

Substitute 16 for d₁.

1/2 ⋅ (16 ⋅ d₂)  =  192

8 ⋅ d₂  =  192

Divide each side by 8.

d₂  =  24 cm

So, the length of the other diagonal is 24 cm. 

4. Answer :

Area of the rhombus  =  120 cm²

1/2 ⋅ (d₁d₂)  =  120

Substitute 10 for d₁ and (7x + 3) for d₂. 

1/2 ⋅ [10(7x + 3)]  =  120

5(7x + 3)  =  120

Divide each side by 5. 

7x + 3  =  24

Subtract 3 from each side. 

7x  =  21

Divide each side by 7.

x  =  3

5. Answer :

In the rhombus shown above,

d₁  =  8 + 8  =  16 units

d₂  =  x + x  =  2x units

Given : Area of the rhombus is 48 square inches. 

Then, 

1/2 ⋅ (d₁d₂)  =  48

Substitute 16 for d₁ and 2x for d₂.

1/2 ⋅ (16 ⋅ 2x)  =  48

8 ⋅ 2x  =  48

16x  =  48

Divide each side by 16.

x  =  3

6. Answer :

Measure the lengths of the diagonals AC and BD.  

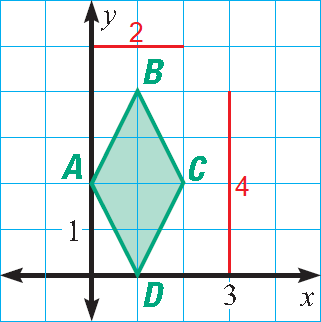
The lengths of the diagonals are  4 units and 2 units. 

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 4 for d₁ and 2 for d₂.

=   1/2 ⋅ (4 ⋅ 2)

=   2 ⋅ 2

=  4 

So, area of the rhombus is 4 square units.

7. Answer :

Let A, B, C and D be the vertices of the rhombus. 

The diagonals of a rhombus will be perpendicular and they will bisect each other. 

Then, we have

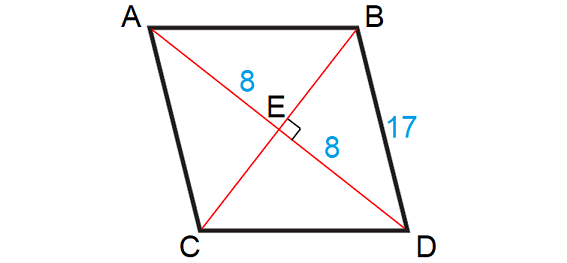
In the above rhombus, consider the right angled triangle BDE. 

By Pythagorean Theorem, 

BD²  =  BE² + DE²

17²  =  BE² + 8²

289  =  BE² + 64

Subtract 64 from each side. 

225  =  BE²

15²  =  BE²

15  =  BE

Then, 

EC  =  15

Length of the diagonal BC : 

BC  =  BE + EC

BC  =  15 + 15

BC  =  30 units

So, the lengths of the diagonals are 16 units and 30 units. 

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 16 for d₁ and 30 for d₂.

=   1/2 ⋅ (16 ⋅ 30)

=   8 ⋅ 30

=  240 

So, area of the rhombus is 240 square units.

8. Answer :

Area of a rhombus = 150 cm²

Length of one diagonal = 10 cm

Let x be the length of other diagonal.

(1/2) ⋅ x ⋅ 10 = 150

5x = 150

x = 150/5

x = 30

So, the length of other diagonal is 30 cm. Option b is correct.

9. Answer :

Area of a rhombus = 25 cm²

Let x be the length of one diagonal. Then the other diagoanl will be 2x.

(1/2) ⋅ x ⋅ (2x) = 25

x² = 25

x = 5 cm

2x = 2(5) ==> 10 cm

Sum of the diagonal = 5 + 10

= 15 cm

So, option c is correct.

10. Answer : 

The pereimeter of the rhombus = 56 m

height = 5 m

Let x be the side length of rhombus.

4x = 56

x = 56/4

x = 14 m

Area of rhombus = base x height

= 14 x 5

= 70 m²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.