AREA OF QUADRILATERAL WHEN FOUR VERTICES ARE GIVEN

Let us consider the quadrilateral ABCD shown below. 

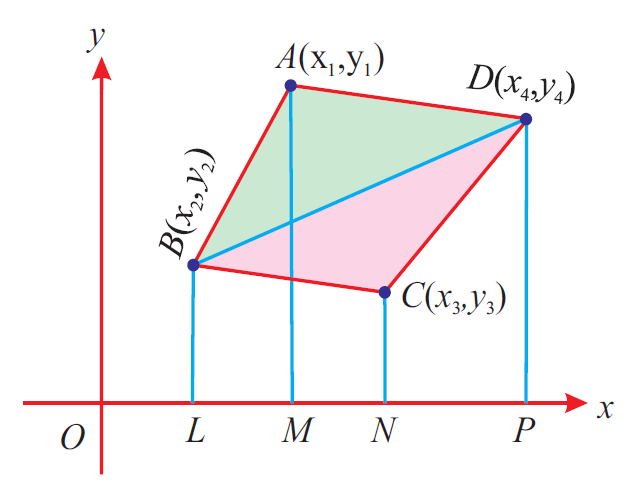
In the above quadrilateral, A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) and D(x₄, y₄) are the vertices.

To find area of the quadrilateral ABCD, now we have take the vertices A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) and D(x₄, y₄) of the quadrilateral ABCD in order (counter clockwise direction) and write them column-wise as shown below. 

Add the diagonal products x₁y₂, x₂y₃, x₃y₄ and x₄y₁ are shown in the dark arrows.

(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) -----(1)

Add the diagonal products x₂y₁, x₃y₂, x₄y₃ and x₁y₄ are shown in the dotted arrows.

(x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄) -----(2)

Subtract (2) from (1) and multiply the difference by 1/2 to get area of the quadrilateral ABCD.

So, area of the quadrilateral ABCD is

=  (1/2) ⋅ {(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁)

- (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)}

Problem :

Find the area of the quadrilateral whose vertices are

(-4, -2), (-3, -5), (3, -2) and (2, 3)

Solution : 

Let A(-4, -2), B(-3, -5), C(3, -2) and (2, 3).

Plot A, B, C and D in a rough diagram and take them in counter-clockwise order.

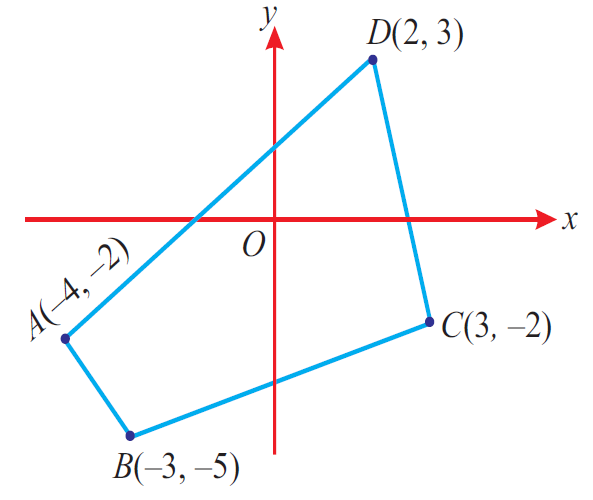
Then,

(x₁, y₁)  =  (-4, -2)

(x₂, y₂)  =  (-3, -5)

(x₃, y₃)  =  (3, -2)

(x₄, y₄)  =  (2, 3)

Area of triangle ABC is 

=  (1/2) ⋅ {(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁)

- (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)}

=  (1/2) x  {[20 + 6 + 9 - 4] - [6 - 15 - 4 - 12]}

=  (1/2) x  {[31] - [-25]}

=  (1/2) x  {31 + 25}

=  (1/2) x  56

=  28

So, area of the given quadrilateral is 28 square units. 

Note : 

If you get the area of a quadrilateral as a negative value, take it as positive.

Because, the area of the quadrilateral is never negative. That is, we always take the area of quadrilateral as positive.

Practice Questions

Find the area of the each quadrilateral whose vertices are

(i)  (6, 9), (7, 4), (4, 2) and (3, 7).

(ii)  (-3, 4), (-5, -6), (4, -1) and (1, 2)

(iii)  (-4, 5), (0, 7), (5, -5) and (-4, -2)

Answers :

(i)  17 square units.

(ii)  43 square units

(iii)  60.5 square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.