AREA CONVERSION CHART

Converting Units for Area or Volume :

• To convert units for area, multiply the area by the square of the conversion factor.
• To convert units for volume, multiply the volume by the cube of the conversion factor.

Problem 1 :

The painting Fracture by Benedict Gibson has an area of 2880 square inches. What is the area of the painting in square feet?

Solution :

1 feet = 12 inches 

1 square feet = 12² 

= 144 square inches

1 square inch = 1/144 ft

2880 square inch = 2880 x (1/144) square ft

= 2880/144

= 20 square feet

Problem 2 :

The painting Busy Market by Haitian painter Frantz Petion has an area of 6 square feet. What is the area of the painting in square inches?

Solution :

1 feet = 12 inches

1 square feet = 144 square inches

6 square feet = 6 x 144

= 864 square inches

So, area of painting is 864 square inches.

Problem 3 :

Shown is a rectangle with length 3m and width 2m

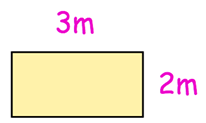
(a) Find the area of the rectangle in m²

(b) What is the length of the rectangle in cm?

(c) What is the width of the rectangle in cm?

(d) Find the area of the rectangle in cm²

(e) Fill in the missing number using your answers to (a) and (d)

1 m² = ____ cm²

Solution :

Length = 3 m

Width = 2 m

a) Area of rectangle = length x width 

= 3 x 2

= 6 m²

b)

1 m = 100 cm

3 m = 300 cm

So, length of the rectangle is 300 cm.

c)  

2 m = 200 cm.

So, width of the rectangle is 200 cm

d) Area of rectangle 

1 m = 100 cm

1 m² = 100 x 100

= 10000 cm²

e)  1 m² = 10000 cm²

Problem 4 :

Shown below are three shapes (not drawn accurately).

List the shapes in order of area, from smallest to greatest.

Solution :

Area of shape A :

= 3 x 2

= 6 m²

Area of shape B :

= 45000 cm²

Converting into m²

1 m = 100 cm

1 m² = 10000 cm²

= 45000/10000

= 4.5 m²

Area of shape C :

400 cm = 4 m

area = 4 x 0.3

= 1.2 m²

Area of shape from smallest to greatest :

Shape C < Shape B < Shape A

Problem 5 :

Tommy has been asked to changed 800 cm² into m² He says: “since there are 100 centimetres in 1 metres, the answer is 8 m²” Explain why Tommy is incorrect.

Solution :

100 centimetres = 1 metre

1 m = 100 cm

1 m² = 10000 cm²

8 m = 800 cm

8 m² = 80000 cm²

So, he is incorrect.

Problem 6 :

Rebecca is tiling her kitchen loor. The floor is a rectangle, measuring 8 m by 6 m. Each tile is a square measuring 20 cm by 20 cm. The tiles are sold in boxes of 10 and each box costs $8.50 Work out the total cost of the tiles needed for the kitchen

Solution :

Area of rectangular floor = 8 x 6

= 48 m²

1 m = 100 cm

1 m² = 10000 cm²

48 m² = 480000 cm²

Area of square tile = 20 x 20

= 400 cm²

Number of tiles needed = 480000/400 

= 1200 tiles

1 box consists of 10 tiles

= 1200 / 10

= 120 boxes

Cost of each box = $8.50

Cost of 120 boxes = 120 x 8.50

= $1020

So, the required cost is $1020.

Problem 7 :

Mrs Jones is tiling her kitchen floor. Each kitchen tile measures 20 cm by 20 cm. The floor measures 3 m wide and 5 m long. The tiles are sold in boxes of 10. Each box costs £6 Work out the total cost of the tiles needed for the kitchen floor

Solution :

Area of rectangular floor = 3 x 5

= 15 m²

1 m = 100 cm

1 m² = 10000 cm²

15 m² = 150000 cm²

Area of square tile = 20 x 20

= 400 cm²

Number of tiles needed = 150000/400 

= 375 tiles

1 box consists of 10 tiles

= 375 / 10

= 37.5

= 38 boxes

Cost of each box = $6

Cost of 38 boxes = 38 x 6

= $228

So, the required cost is $228.

Problem 8 :

What would be the cost of resurfacing a 50 m by 32 m gymnasium floor with a rubberised compound costing $35.60 a square metre?

Solution :

Area of floor = 50 x 32

= 1600 m²

Cost per square meter = $35.60

Required cost = 35.60 x 1600

= $56960

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.