AREA BOUNDED BY TWO PARABOLAS

Example 1 :

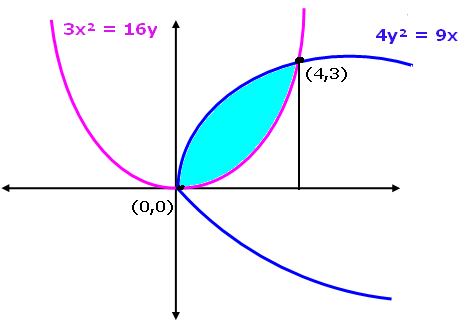
Find the area bounded by two parabolas,

4y²  =  9x and 3x²  =  16y

Solution :

First we need to draw the rough sketch of two parabolas to find the point of intersection.

4y²  =  9x  ------ (1)

3x²  =  16y ------ (2)

4y²  =  9x

y²  =  9x/4 

y  =  3√x/2

y  =  (3/2) √x

3x²  =  16y

y  =  3x²/16

By applying the value of y in the equation y²  =  9x/4.

(3x²/16)²  =  9x/4

 9x⁴/256  =  9x/4 

 x⁴/x  =  (9 ⋅256)/(4 ⋅ 9)

x³  =  256/4

x³  =  64

x³  =   4³ 

x  =  4

By applying the value x = 4 in (1) or (2) we get the value of y

y  =  3(4)²/16

y  =  3

Therefore, the two parabolas are intersecting at the point  (0, 0) and (4, 3).

=  (3/2)[x^(3/2)/(3/2)] - (3/16) [ x^3/3 ]

=  { (3/2) [ 4^(3/2)/(3/2)]- (3/16) [4^3/3] } - 0

=  { [ (3/2) ( 4 √4 ) x (3/2) ]- (3/16) [64/3] } - 0

=  4 (2)-4

=  8-4

=  4  square units

Therefore the required area  =  4 square units.

Example 2 :

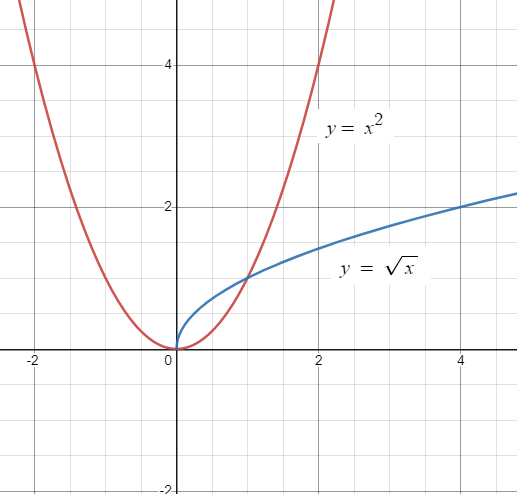
Find the area of the region bounded by the two parabolas 

y  =  x² and y²  =  x.

Solution :

y  =  x² -----(1)

y²  =  x

y  =  √x -----(2)

x²  =  √x

x⁴  =  x

x⁴ - x  =  0

x(x³-1)  =  0

x  =  0 and x  =  1

y  =  1

Point of intersection is at (0, 0) and (1, 1).

Required area  =  Integral 0 to 1 (√x - x²) dx

=  [x^3/2/(3/2) - x³/3] 0 to 1

=  0-(2/3) + 1/3

=  1/3 - 2/3

=  1/3 square units.

Example 3 :

The area between x = y² and x = 4 is divided into two equal parts by the line x = a, find the value of a.

Solution :

x = y²

From the given equation, it is clear that the parabola is symmetric about x-axis it is open rightward parabola.

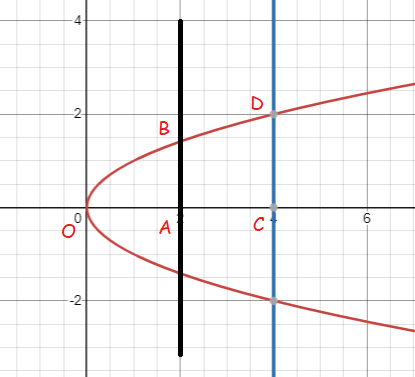
Area of OAB = Area of ACDB

Integral 0 to a √x dx = integral a to 4 √x dx

[x^(3/2)/(3/2)] limits are 0 and a = [x^(3/2)/(3/2)] limits are a to 4

x^(3/2) limits are 0 and a = x^(3/2) limits are a to 4

a^(3/2) - 0 = 4^(3/2) - a^(3/2)

2a^(3/2) = (2^2)^(3/2)

2a^(3/2) = 2³

a^(3/2) = 8/2

a^3/2 = 4

a = 4^2/3

Example 4 :

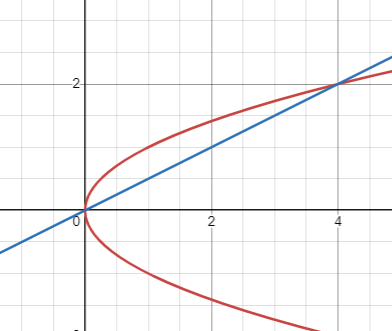
The area of the region bounded by parabola y² = x and the straight line 2y = x is

Solution :

y² = x ------(1)

2y = x ------(2)

(1) = (2)

y² = 2y

y² - 2y = 0

y(y - 2) = 0

y = 0 and y = 2

Applying these values one by one, we get

x = 2(0) ==> 0

x = 2(2) ==> 4

So, the points of intersecting of these two curves are (0, 0) and (4, 2)

Using x values as limits, to figure out area in between these two curves, we have derive the function for y.

y = √x and y = x/2

= Integral 0 to 4 [√x - (x/2)] dx

= [x^(3/2) / (3/2) - (x²/2)] limits are 0 to 4

= [(2/3) x^(3/2) - (x²/4)] limits are 0 to 4

= (2/3) 4^(3/2)  - (4²/4) 

= (2/3) 8 - 4

= (16/3) - 4

= (16 - 12) / 3

= 4/3 square units.

Example 5 :

The area of the region bounded by the curve y = x² and the line y = 16

Solution :

The parabola is symmetric about y-axis and it opens upward.

To find the point of intersection of these two curves, 

y = x² ------(1)

y = 16 ------(2)

(1) = (2)

x² = 16

x = 4 and -4

So, the point of intersections are (4, 16) and (-4, 16).

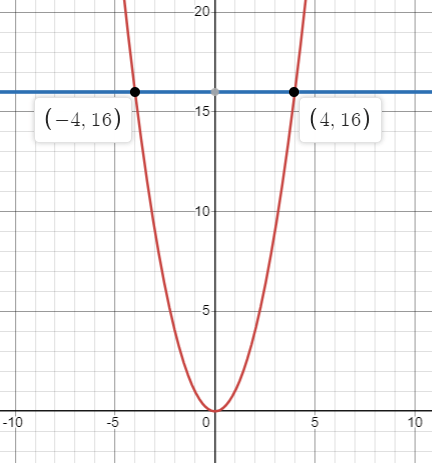
= integral -4 to 4 (16 - x²) dx

= (16x -x³/3) limits are -4 to 4

= 16(-4) - (-64/3) - 16(4) + 64/3

= -64 + (64/3) - 64 + 64/3

= -128 + (128/3)

= (-384 + 128)/3

= 256/3 square units.

Example 6 :

The area of the region bounded by the curve x² = 4y and the line x = 4y - 2

Solution :

x² = 4y ------(1)

x = 4y - 2 ------(2)

To find point of intersecting these two curves, (1) = (2)

√4y  = 4y - 2

4y = (4y - 2)²

4y = 16y² - 16y + 4

16y² - 16y - 4y + 4 = 0

16y² - 20y + 4 = 0

4y² - 5y + 1 = 0

4y² - 4y - 1y + 1 = 0

4y(y - 1) - 1(y - 1) = 0

(4y - 1)(y - 1) = 0

y = 1/4 and y = 1

x = 4y - 2

Applying y = 1/4, we get x = 4(1/4) - 2 ==> -1

Applying y = 1, we get x = 4(1) - 2 ==> 2

So, the point of intersections are (-1, 1/4) and (2, 1).

From (1) and (2)

x²/4 = y ------(1)

(x + 2)/4 = y ------(2)

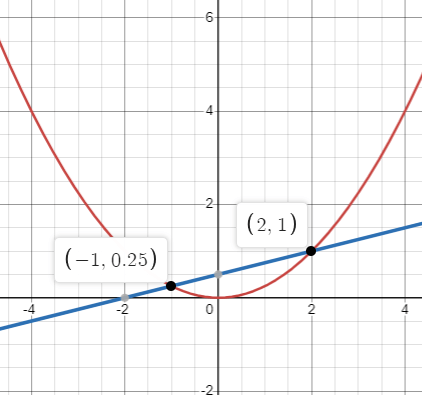
= integral -1 to 2 (16 - x²) dx

= (16x -x³/3) limits are -4 to 4

= 16(-4) - (-64/3) - 16(4) + 64/3

= -64 + (64/3) - 64 + 64/3

= -128 + (128/3)

= (-384 + 128)/3

So, 9/8 square units is the answer.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.