ALGEBRA PRACTICE PROBLEMS WORKSHEET FOR GRADE 10
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
(1) Solve (1/3) (x + y −5) = y − z = 2x −11 = 9−(x +2z)
(2) One hundred and fifty students are admitted to a school. They are distributed over three sections A, B and C. If 6 students are shifted from section A to section C, the sections will have equal number of students. If 4 times of students of section C exceeds the number of students of section A by the number of students in section B, find the number of students in the three sections. Solution
(3) In a three-digit number, when the tens and the hundreds digit are interchanged the new number is 54 more than three times the original number. If 198 is added to the number, the digits are reversed. The tens digit exceeds the hundreds digit by twice as that of the tens digit exceeds the unit digit. Find the original number.
(4) Find the least common multiple of xy(k2 +1)+k(x2 + y2) and xy(k2 −1)+k(x2 −y2) Solution
(5) Find the GCD of the following by division algorithm
2x4 +13x3 +27x2 + 23x + 7 , x3 + 3x2 + 3x + 1 , x2 + 2x + 1
(6) Reduce the given Rational expressions to its lowest form
(i) (x3a - 8)/(x2a + 2xa + 4) Solution
(ii) (10x3 - 25x2 + 4x - 10)/(-4 - 10x2) Solution
(7) Simplify
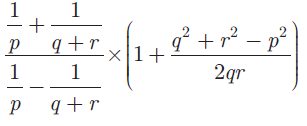
(8) Arul, Ravi and Ram working together can clean a store in 6 hours. Working alone, Ravi takes twice as long to clean the store as Arul does. Ram needs three times as long as Arul does. How long would it take each if they are working alone? Solution
(9) Find the square root of 289x4 −612x3 + 970x2 −684x + 361. Solution
(10) Solve √(y + 1) + √(2y −5) = 3 Solution
(11) A boat takes 1.6 hours longer to go 36 kms up a river than down the river. If the speed of the water current is 4 km per hr, what is the speed of the boat in still water?
(12) Is it possible to design a rectangular park of perimeter 320 m and area 4800 m2 ? If so find its length and breadth. Solution
(13) At t minutes past 2 pm, the time needed to 3 pm is 3 minutes less than t2/4. Find t. Solution
(14) The number of seats in a row is equal to the total number of rows in a hall. The total number of seats in the hall will increase by 375 if the number of rows is doubled and the number of seats in each row is reduced by 5. Find the number of rows in the hall at the beginning Solution
(15) If a and b are the roots of the polynomial f(x) = x2 −2x + 3, find the polynomial whose roots are
(i) α + 2, β + 2 Solution
(ii) (α - 1)/(α + 1), (β - 1)/(β + 1) Solution
(16) If –4 is a root of the equation x2 + px −4 = 0 and if the equation x2 + px +q = 0 has equal roots, find the values of p and q. Solution
(17) Two farmers Senthil and Ravi cultivates three varieties of grains namely rice, wheat and ragi. If the sale (in ₹) of three varieties of grains by both the farmers in the month of April is given by the matrix.
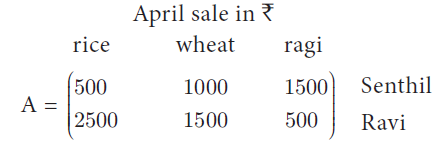
and the May month sale (in ₹) is exactly twice as that of the April month sale for each variety.
(i) What is the average sales of the months April and May.
(ii) If the sales continues to increase in the same way in the successive months, what will be sales in the month of August? Solution
(18)
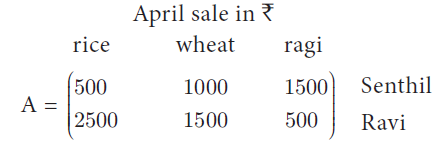
(19) Given
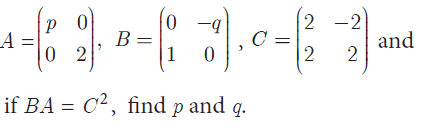
(20)
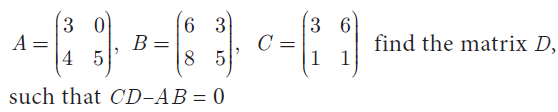
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


