WORKSHEET ON ARC LENGTH AND AREA OF SECTOR

Question 1 :

Find the length of the arc that is bolded. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

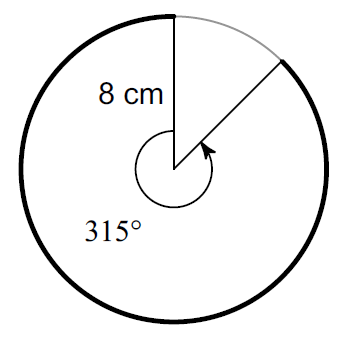
Question 2 :

In the diagram given below, if QRS is a central angle and m∠QRS = 81°, m∠SRT = 115°, and radius is 5 cm, then find the length of the arc QST. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

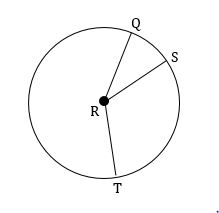
Question 3 :

If m∠LMN = 19° and radius is 15 inches, then find the length of arc LN. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

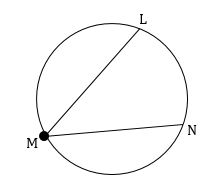
Question 4 : 

Find the length of the arc highlighted in red color. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

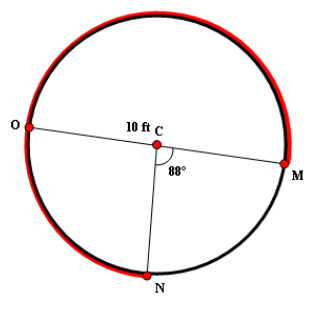
Question 5 :

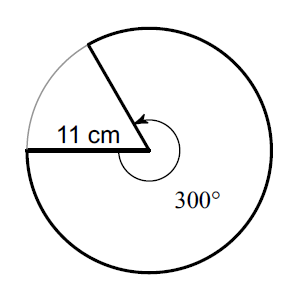
Find the area of the sector that is outlined with the bold line. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Question 6 :

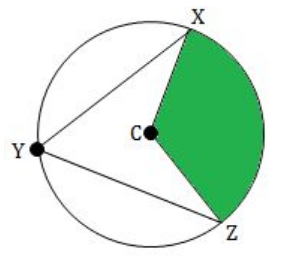
In circle C, if XCZ is a central angle and XYZ is an inscribed angle and m∠XYZ  =  58° and radius is 10 inches. Find the area of sector XCZ. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Question 7 :

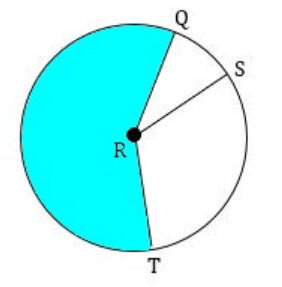
If QRS is a central angle and m∠QRS = 46°, m∠SRT = 80°, and diameter is 4 inches, then find the area of the shaded sector. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Detailed Answer Key

Question 1 :

Find the length of the arc that is bolded. (Take π ≈ 3.14    and round your answer to one decimal place, if necessary)

Solution :

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2πr

Substitute r  =  8, arc Measure  =  315° and π  ≈  3.14.

≈  (315° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 8

=  44

So, the length of the arc is about 44 cm.

Question 2 :

In the diagram given below, if QRS is a central angle and m∠QRS = 81°, m∠SRT = 115°, and radius is 5 cm, then find the length of the arc QST. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Solution :

To find the length of the arc QST, first we have to find the arc measure QST or the central angle m∠QRT. 

m∠QRT  =  m∠QRS + m∠SRT

m∠QRT  =  81° + 115°

m∠QRT  =  196°

The formula to find the arc length is

=  (Central Angle / 360°) ⋅ 2πr

Substitute r  =  5, Central Angle  =  196° and π  ≈  3.14.

≈  (196° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 5

=  17.1

So, the length of the arc is about 17.1 cm.

Question 3 :

If m∠LMN = 19° and radius is 15 inches, then find the length of arc LN. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Solution :

To find the length of the arc LN, first we have to find the arc measure LN. 

By Inscribed Angle Theorem, we have

1/2 ⋅ Arc Measure  =  m∠LMN

Multiply both sides by 2. 

Arc Measure  =  2 ⋅ m∠LMN

Arc Measure  =  2 ⋅ 19°

Arc Measure  =  38°

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2πr

Substitute r  =  15, Arc Measure  =  38° and π  ≈  3.14.

≈  (38° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 15

=  9.9

So, the length of the arc is about 9.9 inches.

Question 4 : 

Find the length of the arc highlighted in red color. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Solution :

From the given diagram, we have

m∠MCN + Measure of arc MON  =  360°

Plug m∠MCN  =  88°

88° + Measure of arc MON  =  360°

Subtract 88° from both sides. 

Measure of arc MON  =  272°

Given : Diameter is 4 inches.

Then, the radius is

=  Diameter / 2

=  10 / 2

=  5 ft

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2πr

Substitute r  =  5, Arc Measure  =  272° and Π  ≈  3.14.

≈  (272° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 5

=  23.7 ft

So, the length of the arc is about 23.7 ft.

Question 5 :

Find the area of the sector that is outlined with the bold line. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Solution :

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Substitute r  =  11, θ  =  300° and π  ≈  3.14.

≈  (300° / 360°) ⋅ 3.14 ⋅ 11²

=  316.7

So, the area of the given sector is about 316.7 cm².

Question 6 :

In circle C, if XCZ is a central angle and XYZ is an inscribed angle and m∠XYZ  =  58° and radius is 10 inches. Find the area of sector XCZ. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Solution :

By Inscribed Angle Theorem, we have

1/2 ⋅ m∠XCZ  =  m∠XYZ

Multiply both sides by 2.

m∠XCZ  =  2 ⋅ m∠XYZ

Given : m∠XYZ  =  58°.

Then, we have

m∠XCZ  =  2 ⋅ 58°

m∠XCZ  =  116°

So, the central angle θ is 116°.

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Substitute r  =  10, θ  =  116° and Π  ≈  3.14.

≈  (116° / 360°) ⋅ 3.14 ⋅ 10²

=  101.2

So, the area of sector XCZ is about 101.2 in².

Question 7 :

If QRS is a central angle and m∠QRS = 46°, m∠SRT = 80°, and diameter is 4 inches, then find the area of the shaded sector. (Take π ≈ 3.14 and round your answer to one decimal place, if necessary)

Solution :

Given : m∠QRS  =  46° and m∠SRT  =  80°.

Then, we have

m∠QRS + m∠SRT  =  46° + 80°

m∠QRS + m∠SRT  =  126°

Measure of central angle of the shaded region :

m∠QRT  =  360° - 126°

m∠QRT  =  234°

Radius of the circle :

Radius  =  Diameter / 2

Radius  =  4 / 2

Radius  =  2 inches

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Substitute r  =  2, θ  =  234° and Π  ≈  3.14

≈  (234° / 360°) ⋅ 3.14 ⋅ 2²

=  8.2

So, the area of the shaded sector is about 8.2 in².

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

If you have any feedback about our math content, please mail us : 

v4formath@gmail.com

We always appreciate your feedback. 

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6