PRACTICE PROBLEMS FOR RHOMBUS
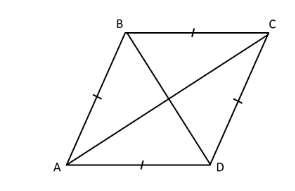
(1) Examine whether the given points
A (2, -3), B (6, 5), C (-2, 1) and D (-6, -7)
forms a rhombus. Solution
(2) Three vertices of a rhombus taken in order are
(2, −1),(3, 4) and (−2, 3)
find the fourth vertex. Solution
(3) Assume quadrilateral EFGH is a rhombus. If the perimeter of EFGH is 24 and the length of diagonal EG = 10, what is the length of diagonal FH? Solution
(4) If the area of a rhombus is 112 cm2 and one of its diagonal is 14 cm find its other. Solution
(5) The length of diagonal are ratio 5:4 area of rhombus is 2250 cm2 find the length of diagonals. Solution
(6) If opposite angles of a rhombus are (2x)° and (3x-40)° then value of x is ? Solution
(7) ABCD is a rhombus in which AB is 3x-2, AC is 4x+4 and BD is 2x. Find x.
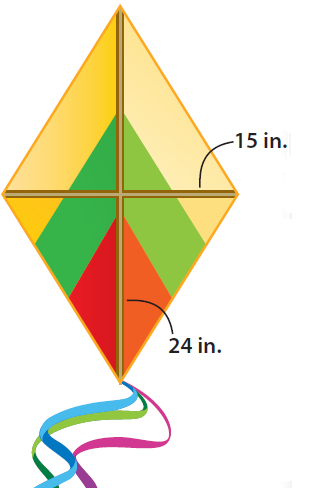
(8) Cedric is constructing a kite in the shape of a rhombus. The spars of the kite measure 15 inches and 24 inches. How much fabric will Cedric need for the kite ?
(9) A kite in the shape of a rhombus has diagonals that are 25 inches long and 15 inches long. What is the area of the kite? Solution
(10) The diagonals of a rhombus are 12 in. and 16 in. long. The length of a side of the rhombus is 10 in. What is the height of the rhombus ? Solution

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Factoring Quadratic Trinomials Worksheet
Apr 25, 24 07:47 PM
Factoring Quadratic Trinomials Worksheet -
Factoring Quadratic Trinomials
Apr 25, 24 07:03 PM
Factoring Quadratic Trinomials - Methods - Solved Examples -
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems

